
What is Quadratic Equation?
The definition of
quadratic equation is: “A second degree equation in one variable is known as a Quadratic Equation.”
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Quadratic Equation Examples
x2 – 25 = 0, 4x2 – 81 = 0, x2 + 3x + 2 = 0, 2x2 – 7x – 15 = 0 are some of the examples of quadratic equations.
Standard Form of Quadratic Equation
A quadratic equation of the form ax2 + bx + c = 0
where a, b and c are constant and a ≠ 0, is called Standard Form of Quadratic Equation. The standard form of
quadratic equation is also known as General
Form of Quadratic Equation.
3x2 – 5x + 2 = 0 is an example of quadratic equation
in standard form.
Types of Quadratic Equation
On the basis of their
forms, quadratic equations are of two types:
1. Pure Quadratic Equation
2. Adfected Quadratic Equation
Pure Quadratic Equation
A quadratic equation of the form ax2 + c = 0 where
the middle term bx is missing, is known as a Pure Quadratic Equation. For example: x2 – 9 = 0, 2x2
– 5 = 0 etc. are pure quadratic equations.
Adfected Quadratic Equation
A quadratic equation in its standard form is known as an Adfected Quadratic equation. For
examples: x2 + 9x + 14 = 0, 2x2 + 5x – 3 = 0 etc. are the
adfected quadratic equations.
Solving Quadratic Equation
Solving a quadratic
equation means finding the values of the variable that satisfies the quadratic
equation.
Solution of quadratic equations
The values of the
variable that satisfies the quadratic equation are called the solution of the quadratic equation. A
quadratic equation has degree 2, therefore there are 2 solutions of a quadratic
equation.
Two solutions of a
quadratic equation are called the roots of the quadratic equation. The roots of
a quadratic equation ax2 + bx + c = 0 may be distinct and real,
equal and real, or both imaginary (complex number) according to the conditions
given below:
1.
When b2 >
4ac, the roots are distinct and real number.
2.
When b2 = 4ac,
the roots are equal and real number.
3.
When b2 <
4ac, roots are imaginary or there is no real solution.
Ways to Solve Quadratic Equations
We can solve a quadratic equation by following three ways:
1.
By factoring quadratic
equation method
2.
By completing square
method
3.
By using quadratic
equation formula
Solving Quadratic Equations by Factoring
This is the easiest method to solve a quadratic equation. In
this method, we factorize the quadratic expression into the product of two
linear binomial factors. Then, by applying the zero product property, we can
find the solutions of the quadratic equation.
What is zero product property?
If the product of any two numbers is 0, then either one or both
of the numbers must be 0. This is called Zero
Product Property. i.e. if p×q = 0, then either p = 0 or q = 0.
Therefore, after
factoring the quadratic expression, we equate each linear binomial factor with
0 and solve it to get the value of variables.
Here are the steps for solving quadratic equations by factoring:
Step 1: Remove the brackets of
fractions if there is any in the equation.
Step 2: Simplify and reduce the
equation in the form of ax2 + bx + c = 0.
Step 3: Factorize the left-hand
side into two factors.
Step 4: Use the above property of
numbers and write each factor equal to 0.
Step 5: Solve both factors and
get two values of the variable.
Here are the examples of solving quadratic equations by
factoring:
Worked Out Examples
Example 1: Calculate roots of
quadratic equation x2 – 9 = 0.
Solution: Here,
x2 – 9 = 0
or, x2 – 32 = 0
or, (x + 3)(x – 3) = 0
∴ Either, x + 3 = 0 or, x = - 3
Or, x – 3 =
0 or, x = 3
∴ x = 3, –3 Answer.
Example 2: Calculate roots of
quadratic equation 2x2 = 8.
Solution: Here,
2x2 = 8
or, x2 = 8/2
or, x2 = 4
or, x2 – 4 = 0
or, x2 – 22 = 0
or, (x + 2)(x – 2) = 0
∴ Either, x + 2 = 0 or, x = - 2
Or, x – 2 =
0 or, x = 2
∴ x = 2, –2 Answer.
Example 3: Calculate roots of quadratic equation x2
– x – 6 = 0.
Solution: Here,
x2 – x – 6 = 0
or, x2 – (3 – 2)x – 6 = 0
or, x2 – 3x + 2x – 6 = 0
or, x(x – 3) + 2(x – 3) = 0
or, (x – 3)(x + 2) = 0
∴ Either, x – 3 = 0 or, x =
3
Or, x + 2 =
0 or, x = –2
∴ x = 3, –2 Answer.
Example 4: Find
the roots of the following quadratic equation by factorisatione: x2 – 3ax + 2bx – 6ab = 0.
Solution: Here,
x2 – 3ax + 2bx – 6ab = 0
or, x(x – 3a) + 2b(x – 3a) = 0
or, (x – 3a)(x + 2b) = 0
∴ Either, x – 3a = 0 or, x = 3a
Or, x + 2b = 0 or, x = -2b
∴ x = 3a, -2b Answer.
Example 5: Find the roots of the following quadratic equation by factorisation:
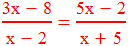
Solution: Here,

or, (3x – 8)(x + 5) = (5x – 2)(x – 2)
or, 3x2 + 15x – 8x – 40 = 5x2 – 10x – 2x + 4
or, 3x2 + 7x – 40 – 5x2 + 12x – 4 = 0
or, -2x2 + 19x – 44 = 0
or, -(2x2 – 19x + 44) = 0
or, 2x2 – 11x – 8x + 44 = 0/-1
or, x(2x – 11) – 4(2x – 11) = 0
or, (2x – 11)(x – 4) = 0
∴ Either, x – 4 = 0 or, x =
4
Or, 2x – 11 =
0 or, 2x = 11 or x = 11/2
∴ x = 4, 11/2 Answer.
Example 6: Find the roots of the following quadratic equation by factorisation:

Solution: Here,

or, 5(x2 – 1) = 24x
or, 5x2 – 5 = 24x
or, 5x2 – 24x – 5 = 0
or, 5x2 – (25 – 1)x – 5 = 0
or, 5x2 – 25x + x – 5 = 0
or, 5x(x – 5) + 1(x – 5) = 0
or, (x – 5)(5x + 1) = 0
∴ Either, x – 5 = 0 or, x =
5
Or, 5x + 1 =
0 or, 5x = –1 or x = –1/5
∴ x = 5, –1/5 Answer.
Some Questions and Answers
What is quadratic?
Answer:
The meaning of
quadratic is "power 2". It came from the Latin word "quadratum" meaning "square".
What is the meaning of quadratic equation?
Answer:
The meaning of a
quadratic equation is an equation in which there is a quadratic or square of
the variable term in the equation.
What is the standard form of quadratic equation?
Answer:
The standard form of
quadratic equation is ax2 + bx + c = 0.
What is the general form of quadratic equation?
Answer:
The general form of
the quadratic equation is ax2 + bx + c = 0.
What are the roots of a quadratic equation?
Answer:
The roots of a
quadratic equation are the solution of the quadratic equation i.e the values of
the variable that satisfies the quadratic equation.
What is the degree of quadratic equation?
Answer:
The degree of
quadratic equation is 2.
What are quadratic equations used for?
Answer:
The quadratic equations
are used to solve the problems related to the area of rectangular field,
surrounding-path, cross-path in which the length or breadth are given in terms
of variable term, and some conditional problems involving the square of a
variable or the product of two variables along with the sum and/or difference.
What is the formula of quadratic equation?
Answer:
The formula of quadratic equation is:

If you have any questions or problems regarding the Quadratic Equations and Factorization
Method, you can ask here, in the comment
section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: