Quadratic Formula

0 comments

Quadratic Formula

 

A formula to calculate the roots or solutions of a quadratic equation ax2 + bx + c = 0 is known as the Quadratic Formula which is given as,

"x" = ("-b ± " √("b" ^"2" "- 4ac" ))/"2a"

where a is the coefficient of x2, b is the coefficient of x and c is the constant term. We use this formula to find the required solutions (roots) of the given quadratic equation.

Some special conditions:

When b2 > 4ac, there are two distinct real roots.

When b2 = 4ac, there is a single real root.

When b2 < 4ac, there is no real roots.

 


********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************

 

Derivation of Quadratic Formula

 

Consider the general quadratic equation

ax2 + bx + c = 0, where a, b and c are constants and a≠ 0.

Rewriting the given equation as

ax2 + bx = – c

Dividing both sides by the coefficient of x2 i.e. a we get

x2 + " b " /"a" x = – " c " /"a"

In order to make the left-hand side a perfect square, we take half the coefficient of x,

i.e. "b" /"2a" and square it to obtain "b" ^"2" /〖"4a" 〗^"2" . Then adding "b" ^"2" /〖"4a" 〗^"2" to both sides we get, x2 + " b " /"a" x + "b" ^"2" /〖"4a" 〗^"2" = "b" ^"2" /〖"4a" 〗^"2" – " c " /"a" or, x2 + 2.x. "b" /"2a" + ("b" /"2a" )^"2" = ("b" ^"2" "-4ac" )/〖"4a" 〗^"2" or, ("x+ " "b" /"2a" )^"2" = ("b" ^"2" "-4ac" )/〖"4a" 〗^"2"

Taking square root to both sides, we get

or, "x+ " "b" /"2a" = ± √(b^2- 4ac)/2a or, "x" = "- " "b" /"2a" "± " √("b" ^"2" "- 4ac" )/"2a" ∴ "x" = ("-b ± " √("b" ^"2" "- 4ac" ))/"2a"

Hence the Quadratic Formula is derived.


 

Workout Examples

 

Example 1: Solve x2 – 7x + 12 = 0 by using quadratic formula.

Solution: Here,

x2 – 7x + 12 = 0

Comparing this equation with ax2 + bx + c = 0 we get,

a = 1

b = –7

c = 12

Now, by using quadratic formula,

x = ("-b ± " √("b" ^"2" "- 4ac" ))/"2a" = ("-(-7) ± " √(〖"(-7)" 〗^"2" "- 4×1×12" ))/"2×1" = ("7 ± " √("49- 48" ))/"2" = ("7 ± " √("1" ))/"2" = "7 ± 1" /"2" Taking +ve sign, x = "7+ 1" /"2" = " 8 " /"2" = 4 Taking –ve sign, x = "7- 1" /"2" = " 6 " /"2" = 3

 

Example 2: Solve (p – q)x2 + (p + q)x + 2q = 0 by using quadratic formula.

Solution: Here,

(p – q)x2 + (p + q)x + 2q = 0

Comparing this equation with ax2 + bx + c = 0 we get,

a = (p – q)

b = (p + q)

c = 2q

Using quadratic formula,

x = ("-b ± " √("b" ^"2" "- 4ac" ))/"2a" = ("-(p+q) ± " √(〖"(p+q)" 〗^"2" "- 4×(p-q)×2q" ))/"2(p-q)" = ("-p-q ± " √("p" ^"2" "+2pq+" "q" ^"2" "-8pq+8" "q" ^"2" ))/"2(p-q)" = ("-p-q ± " √("p" ^"2" "-6pq+" 〖"9q" 〗^"2" ))/"2(p-q)" = ("-p-q ± " √(〖"(p-3q)" 〗^"2" ))/"2(p-q)" = "-p-q ±(p-3q)" /"2(p-q)" Taking +ve sign, x = "-p-q+p-3q" /"2(p-q)" = "-4q" /"2(p-q)" = "-2q" /"p-q" Taking –ve sign, x = "-p-q-p+3q" /"2(p-q)" = "-2p+2q" /"2(p-q)" = "-2(p+q)" /"2(p-q)" = -1 ∴ x = "-2q" /"p-q" , -1



Example 3: Solve "1" /"x-2" "+" "2" /"x-1" "= " " 6 " /"x" by using quadratic formula. Solution: Here, "1" /"x-2" "+" "2" /"x-1" "= " " 6 " /"x" or, "x-1+2(x-2)" /("x-2" )"(x-1)" "= " " 6 " /"x" or, "x-1+2x-4" /("x" ^"2" "-x-2x+2" ) "= " " 6 " /"x" or, "3x-5" /("x" ^"2" "-3x+2" ) "= " " 6 " /"x"
 

or, 6x2-18x+12 = 3x2-5x

or, 6x2–18x+12–3x2+5x = 0

or, 3x2–13x+12= 0

Comparing this equation with ax2 + bx + c = 0 we get,

a = 3

b = –13

c = 12

Now, by using quadratic formula,

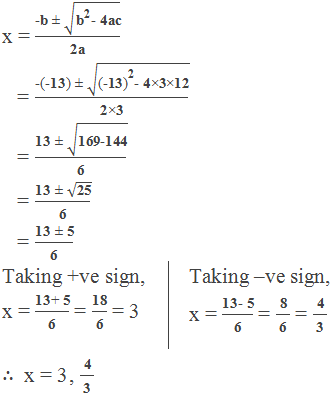
x = ("-b ± " √("b" ^"2" "- 4ac" ))/"2a" = ("-(-13) ± " √(〖"(-13)" 〗^"2" "- 4×3×12" ))/"2×3" = ("13 ± " √("169-144" ))/"6" = ("13 ± " √("25" ))/"6" = "13 ± 5" /"6" Taking +ve sign, x = "13+ 5" /"6" = "18" /"6" = 3 Taking –ve sign, x = "13- 5" /"6" = " 8 " /"6" = " 4 " /"3" ∴ x = 3, " 4 " /"3"

 

If you have any questions or problems regarding the Quadratic Formula, you can ask here, in the comment section below.


 

Was this article helpful? LIKE and SHARE with your friends…

Labels:

0 comments:

Subscribe to: Post Comments (Atom)