Rectangle | What is Rectangle?

Rectangle

 

A quadrilateral having opposite sides equal and each angles 90° (right angle) is called a rectangle.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Or, we can say that a rectangle is a parallelogram with each angle 90°. So, each rectangle is a parallelogram but each parallelogram is not a rectangle.

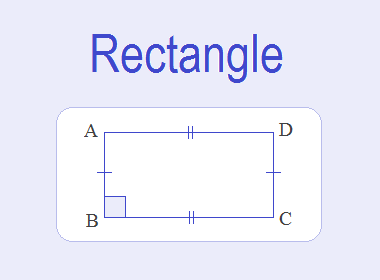
In the given figure of quadrilateral ABCD, opposite sides AB = CD and AD = BC and each angles ∠A, ∠B, ∠C and ∠D are 90°. So ABCD is a rectangle.

 

 

Length and breadth of a rectangle

 

The longer side of the rectangle is taken as length, it is denoted by ‘l’. And, the shorter side is taken as breadth, and it is denoted by ‘b’.

In the given figure of rectangle ABCD,

 

Length (l) = BC = AD

Breadth (b) = AB = CD

 

Diagonals of a rectangle

 

The line joining the opposite vertices of a rectangle or any polygon is called a diagonal. Two diagonals of a rectangle are equal and bisect to each other.

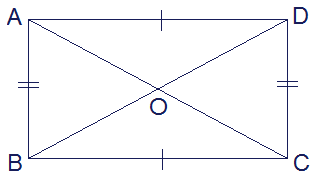
In the given figure of rectangle ABCD. AC and BD are diagonals. They are equal and bisect to each other i.e. AC = BD and AO = CO, BO = DO.

 

The length of diagonal of a rectangle is given by the formula:

Length of diagonal = √(l² + b²)

 

 

Perimeter and Area of Rectangle

 

The perimeter and area of a rectangle are given by the formula:

 

Perimeter of rectangle = 2(l + b)

Area of rectangle = l × b

 

 

Properties of Rectangle

Following are the properties of a rectangle:

 

1.     Opposite sides of a rectangle are equal.

2.     Each angle of a rectangle is 90°.

3.     Opposite sides of a rectangle are parallel.

4.     Diagonals of a rectangle are equal.

5.     Diagonals of a rectangle bisect to each other.

 

 

Worked Out Examples

 

Example 1: Calculate the area and perimeter of the rectangle given below:

Solution:

Here,

In the given rectangle ABCD,

Length (l) = 12 cm

Breadth (b) = 5 cm

 

∴ Area (A) = l × b 

                   = 12cm × 5cm

                   = 60 cm²

And,

∴ Perimeter (P) = 2(l + b)

                   = 2(12cm + 5cm)

                   = 2 × 17cm

                   = 34cm

 

∴ Area = 60cm² and Perimeter = 34cm Ans.

 

 

Example 2: Calculate the area and perimeter of the rectangle given below:

Solution:

Here,

In the given rectangle ABCD,

Diagonal (d) = 5cm

Length (l) = 4cm

 

We know,

l² + b² = d²

i.e.     (4cm)² + b² = (5cm)²

or,     16cm² + b² = 25cm²

or,     b² = 25cm² – 16cm²

or,     b² = 9cm²

or,     b = √(9cm²)

or,     b = 3cm

 

Now,

Area (A) = l × b

                   = 4cm × 3cm

                   = 12 cm²

And,

Perimeter (P) = 2(l + b)

                   = 2(4cm + 3cm)

                   = 2 × 7cm

                   = 14cm

 

∴ Area = 12cm² and Perimeter = 14cm Ans.

 

 

If you have any questions or problems regarding the Rectangle, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…