Section formula is a
formula to calculate the coordinates of any point P(x, y) which divides the
line joining the points A(x1, y1) and B(x2, y2)
in the ratio of m1:m2 internally or externally. Here are
those formulas:
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
(i) If P(x, y) divides AB internally in the ratio of m1:m2,
then the section formula for internal division is given by,

(ii) If P(x, y) divides AB externally in the ratio of m1:m2,
then the section formula for external division is given by,

Derivation of Section Formula
Internal Division
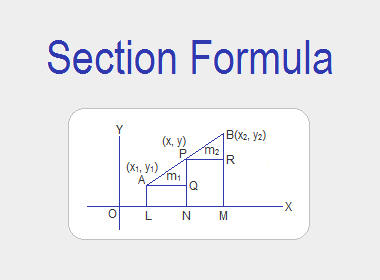
Let A(x1, y1) and B(x2,
y2) be given two points. Let the point P(x, y) divides the line
joining AB internally in the ratio of m1:m2. Then, AP:PB
= m1:m2
Draw perpendiculars AL, PN and BM from A,
P and B respectively to the x-axis. Then, OL = x1, ON = x, OM = x2,
AL = y1, PN = y and BM = y2. Again draw perpendicular AQ
and PR from A and P to the line segments PN and BM respectively.

Then,
AQ =
LN = ON – OL = x – x1
PR =
NM = OM – ON = x2 – x
PQ =
PN – QN = PN – AL = y – y1
BR =
BM – RM = BM – PN = y2 – y
Now,
from the figure, In ΔPQA and ΔBRP,
i.
∠PQA = ∠BRP
---> both right angles
ii.
∠QAP = ∠RPB
---> corresponding angles
iii. ∠APQ = ∠PBR ---> corresponding angles
∴ DPQA ~ DBRP ------> by
AAA axiom

External Division
Let A(x1, y1) and
B(x2, y2) be given two points. Let the point P(x, y)
divides the line joining AB externally in the ratio of m1:m2.
Then, AP:PB = m1:m2
Draw perpendiculars AL, BM and PN from A,
B and P respectively to the x-axis. Then, OL = x1, OM = x2,
ON = x, AL = y1, BM = y2 and PN = y. Again draw
perpendiculars AQ from A to PN and PR
from P to BM produced.

Then,
AQ =
LN = ON – OL = x – x1
PR =
NM = ON – OM = x – x2
PQ =
PN – QN = PN – AL = y – y1
BR =
RM – BM = PN – BM = y – y2
In ΔPQA
and ΔBPR,
i.
∠PQA = ∠BRP
---> both right angles
ii.
∠QAP = ∠RPB
---> corresponding angles
iii. ∠APQ = ∠PBR ---> corresponding angles
∴ DPQA ~ DBRP ------> by
AAA axiom

Note: The
coordinates in the external division are obtained from those of the internal
division by writing – m2 for m2.
Mid-point Formula
If P(x,
y) is the mid-point of the line joining A(x1, y1) and B(x2,
y2), then the point P(x, y) divides the line AB internally in the ratio
of 1:1. Therefore, by applying the section formula for internal division,
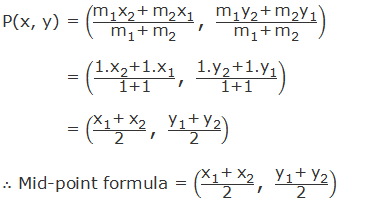
K-formula
If P(x,
y) divides the line joining the points A(x1, y1) and B(x2,
y2) in the ratio of k:1, then,

It is a section formula in terms of k,
which is called K-formula.
It is convenient to let the ratio as k:1 while
solving the problems to find the ratio when the points are given. In such
situations, we use the K-formula. Look at the worked-out examples below.
Centroid Formula
Medians of a triangle intersect at a common point
which is called the centroid of a triangle. If A(x1, y1), B(x2,
y2) and C(x3, y3) are the vertices of a
triangle ABC and G is the median, then the coordinates of centroid G is given
by the following formula,

Proof of Centroid Formula:
Let A(x1, y1), B(x2, y2)
and C(x3, y3) are the vertices of a triangle ABC. D, E
and F are the mid-points of BC, CA and AB respectively. And, medians AD, BE and
CF intersect at point G.

Worked Out Examples
Example 1: Find the co-ordinates of the
point which divides the line joining the points (-3, -2) and (2, 8) in the
ratio of 3:2 internally.

Example 2: What ratio is the line joining
(-3, 4) and (2, -6) divided by the point (-1, 0)?

Example 3: If the points A (6, 4), B
(a, 2), and C (1, -1) are three points on the same straight line, find the ratio
in which the point B divides the line
segment AC and also find the value of a.

Example 4: Find the coordinates of the
points of trisection of the line joining the points M (7, -3) and N (1, 3).
Solution:
Points of
trisection of a line segment joining two points are those points which divides the given line
segment into three equal parts.
Let, P(a, b) and Q(c, d) are the points of trisection of the
line segment joining the points M(7, -3) and N(1, 3). So P(a, b) divides MN in
the ratio of 1:2, and hence,

Hence, the required points of
trisection are P(5, -1) and Q(3, 1).
Example 5: Find the
centroid of the triangle with vertices A(-2, 4), B(11, 15) and C(3, -1).
Solution:
Let G(x, y) be the
centroid of the triangle ABC with vertices A(-2, 4), B(11, 15), and C(3, -1). By
using the formula of centroid,

Hence, the centroid of the
triangle is G(4, 6).
If you have any questions or problems regarding the Section Formula, you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…



0 comments: