Alternate Angles

Alternate Angles

 

Alternate interior angles

When two lines are cut by a transversal then the pair of angles on the opposite sides of the transversal but inside the two lines (i.e. interior angles) are called alternate interior angles.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

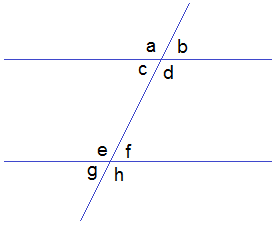
In the given figure ∠c and ∠f, ∠d and ∠e are pairs of alternate angles.

The alternate angles made by a transversal with parallel lines are always equal and are also known as ‘Z’ shaped angles as shown in the figure given below.

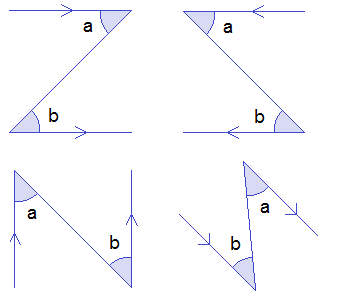
In the figure, ∠a = ∠b as they are alternate (‘Z’ shaped) angles made by the transversal with parallel lines.

 

 

Alternate exterior angles

 

Pair of angles formed on the opposite side of transversal but outside the two lines (i.e. exterior angles) are called alternate exterior angles.

 

Alternate exterior angles are equal if two parallel lines are cut by a transversal line.

In the figure given above, RS is parallel to PQ and EF is a transversal, therefore the alternate exterior angles are equal. i.e. ∠a = ∠c and ∠b = ∠d.

Worked Out Examples

 

Example 1: Find the value of x from the given figure.

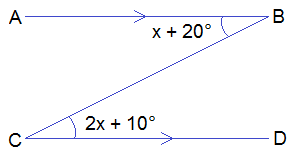
Solution:

Here,

From the figure,

2x + 10° = x + 20° ------> Aternate angles are equal.

or,     2x – x = 20° – 10°

or,     x = 10° Ans.

 

 

Example 2: Find the value of x from the given figure.

Solution:

Here,

From the figure,

6x – 40° = 4x + 50° ------> Aternate exterior angles are equal.

or,     6x – 4x = 50° + 40°

or,     2x = 90°

or,     x = 90°/2

or,     x = 45° Ans.

 

 

Example 3: Find the value of a, b, and c from the given figure.

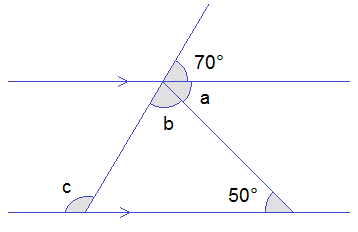
Solution:

Here,

From the figure,

a = 50° ------> Alternate angles.

 

Now,

b + a + 70° = 180° ------> Straight angle.

or,     b + 50° + 70° = 180°

or,     b + 120° = 180°

or,     b = 180° – 120°

or,     b = 60°

 

Again,

c = a + b ------> Alternate angles.

   = 50° + 60°

   = 110°

 

 

If you have any questions or problems regarding the Alternate Angles, you can ask here, in the comment section below.

Was this article helpful? LIKE and SHARE with your friends…