Congruent Triangles
Two triangles are said to be congruent triangles if they are exactly the same by their shapes and sizes.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Two triangles of the same shape are meant three angles of one
triangle are equal to the corresponding three angles of another triangle. And,
two triangles of the same size are meant three sides of one triangle are equal
to the corresponding three sides of another triangle.
The symbol ≅ is used for congruent triangles.
For example:
In the given triangles ABC and PQR, AB = PQ, BC = QR, AC = PR.
Also, ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R. So the triangles ABC
and PQR are congruent. It is written as ΔABC ≅ ΔPQR.
Conditions for Congruency
The following conditions are necessary for the congruency of two triangles.
Condition - 1: Side-Side-Side (SSS)
axiom
When three sides of a triangle are equal to three corresponding sides of another triangle, they are congruent by Side-Side-Side condition. It is called SSS axiom.
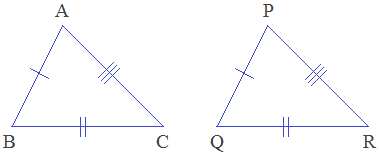
In the given triangles, AB = PQ (S), BC = QR (S), AC = PR (S). Therefore, ΔABC ≅ ΔPQR by SSS axiom.
Condition - 2: Side-Angle-Side
(SAS) axiom
When Side-Angle-Side serially of a triangle are equal to the corresponding Side-Angle-Side serially of another triangle, then the triangles are congruent by Side-Angle-Side condition. It is called SAS axiom.
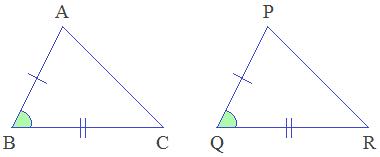
In the given triangles, AB = PQ (S), ∠B = ∠Q (A), BC = QR (S). Therefore, ΔABC ≅ ΔPQR by SAS axiom.
Condition - 3: Angle-Side-Angle
(ASA) axiom
When Angle-Side-Angle serially of a triangle are equal to the corresponding Angle-Side-Angle serially of another triangle, then the triangles are congruent by Angle-Side-Angle condition. It is called ASA axiom.
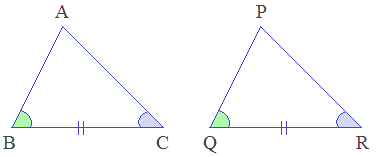
In the given triangles, ∠B = ∠Q (A), BC = QR (S), ∠C = ∠R (A). Therefore, ΔABC ≅ ΔPQR by ASA axiom.
Condition - 4: Right angle-Hypotenuse-Side
(RHS) axiom
In two right-angled triangles, if the hypotenuse and a side of a triangle are equal to the hypotenuse and a side of another triangle, then the triangles are congruent by Right angle-Hypotenuse-Side condition. It is called RHS axiom.
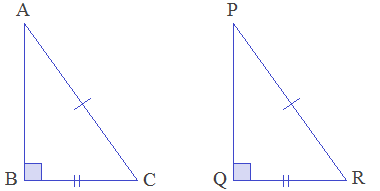
In the given triangles, ∠B = ∠Q = 90° (R), AC = PR (H), BC = QR (S). Therefore, ΔABC ≅ ΔPQR by RHS axiom.
Condition - 5: Side-Angle-Angle (SAA)
axiom
When Side-Angle-Angle serially of a triangle are equal to the corresponding Side-Angle-Angle serially of another triangle, then the triangles are congruent by Side-Angle-Angle condition. It is called SAA axiom.
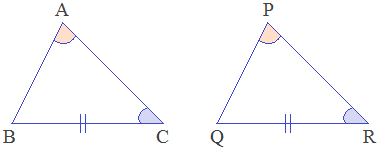
In the given triangles, BC = QR (S), ∠C = ∠R (A), ∠A = ∠P (A). Therefore, ΔABC ≅ ΔPQR by SAA axiom.
Worked Out Examples
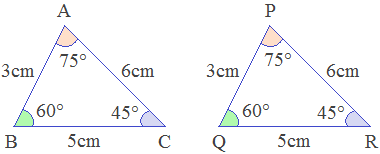
Example 1: In the given figure, state the condition of congruency and write their corresponding sides and angles.
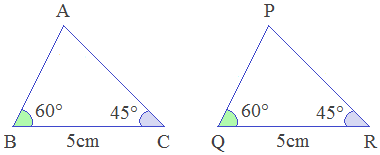
Solution: Here,
In ΔPQR and ΔABC
i.
∠B
= ∠Q
(A) -------> both 60°
ii.
BC = QR (S) -------> both 5cm
iii.
∠C
= ∠R
(A) -------> both 45°
∴ ΔABC ≅ ΔPQR
-------> by ASA axiom
∴ AB = PQ, AC = PR -------> corresponding sides of congruent triangles
∴ ∠A = ∠P -------> corresponding angles of congruent triangles
Example 2: In the given figure, BP = PC, AP⊥ BC, prove that ΔABP≅ ΔAPC, also find the value of a.

Solution: Here,
In ΔABP and ΔAPC
i.
BP = PC (S) -------> given
ii.
∠APB
= ∠APC
(A) -------> both right angles
iii.
AP = AP (S) -------> common side of both triangles
∴ ΔABP ≅ ΔAPC -------> by SAS axiom
∴ AB = AC -------> corresponding sides of congruent triangles
or, 2a + 3 = 5
or, 2a = 5 – 3
or, 2a = 2
or, a = 1
Ans.
Example 3: In the given figure, AP = DP, CP = BP, ∠PAC = 30° and ∠PDB = 40° then,
a.
Prove that ΔAPC≅ ΔDPB
b. Find the values of a, b and y.

Solution: Here,
In ΔAPC and ΔBPD
i.
AP = PD (S) -------> given
ii.
∠APC
= ∠DPB
(A) -------> vertically opposite angles
iii.
PC = PB (S) -------> given
∴ ΔAPC ≅ ΔDPB --------> by SAS axiom
∴ a = 40° ------->
corresponding angles of congruent triangles
∴ b = 30° ------->
corresponding angles of congruent triangles
∴ AC = DB -------> corresponding sides of
congruent triangles
or, y + 3 = 2y
or, 3 = 2y – y
or, y = 3
Ans.
If you have any questions or problems regarding the Congruent Triangles, you can ask here, in the comment section below.
Was this article helpful? LIKE and SHARE with your friends…




0 comments: