
HCF (Highest Common Factor): HCF of given two or more than two numbers is a highest number which can exactly divide the given numbers without any remainder. Among the common factors of those numbers the highest one is the HCF of the numbers.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
For example, 8 is the highest number
which can divide 16, 24 and 32 without any remainder. So 8 is the HCF of 16, 24
and 32.
Here,
The factors of 16, F16 = {1, 2, 4, 8, 16}
The factors of 24, F24 = {1, 2, 3, 4, 6, 8, 12, 24}
The factors of 32, F32 = {1, 2, 4, 8, 16, 32}
Common factors = {1, 2, 4, 8}
The highest common factor = 8
∴ HCF of 16, 24 and 32 is = 8.
Note: If there is no common factor between two or more than two numbers, then HCF is 1. Because 1 is a factor of every number.
HCF can be calculated by using the following methods:
A. Factor listing method
B. Prime factorization
method
C. Division method
Lets find HCF of 24, 42 and 60 by three
different methods:
A. Factor listing method
The factors of 24, F24 = {1, 2, 3, 4, 6, 8, 12, 24}
The factors of 42, F42 = {1, 2, 3, 6, 7, 14, 21, 42}
The factors of 60, F60 = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}
Common factors = {1, 2, 3, 6}
The highest common factor is 6.
∴ HCF = 6
B. Prime factorization method
Here,

∴ 24 = 2 × 2 × 2 × 3
42 = 2 × 3 × 7
60 = 2 × 2 × 3 × 5
The product of the common factors is the
HCF.
∴ HCF = 2 × 3 = 6
C. Division method
To calculate HCF by using division
method, we should apply the following steps:
Step 1: Divide the greater number by the smaller number.
Step 2: Take the remainder as the divisor and divisor as the dividend.
Step 3: Continue the process till we get 0 as the remainder.
Step 4: The last divisor is the HCF of the given numbers.
To find the HCF of 24, 42 and 60, at first we find the HCF of 24 and 42. And then again find HCF of the last divisor i.e. HCF and 60.

Last divisor is the HCF
∴ HCF = 6
Worked Out Example
Example 1: Find the HCF of 125, 275 and
375 by using:
a.
Factor
listing method
b.
Prime
factorization method
c. Division method
Solution:
a. Factor listing method:
Here,
Factors of 125, F125 = {1,
5, 25, 125}
Factors of 275, F275 = {1,
5, 11, 25, 55, 275}
Factors of 375, F375 = {1,
5, 15, 25, 75, 125, 375}
Common factors = {1, 5, 25}
∴ HCF = 25
b. Prime factorization method:
Here,
∴ 125 = 5 × 5 × 5
275 = 5 × 5 × 11
375 = 3 × 5 × 5 ×
5
The product of the common factors is the HCF,
∴ HCF = 5 × 5 = 25
c. Division method:
Here,
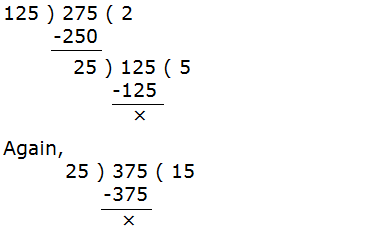
Last divisor is the HCF
∴ HCF = 25
Example 2: Find the greatest number which divides exactly the numbers 250, 450 and 600.
Solution:
The greatest number which divides
250, 450 and 600 exactly is the HCF of the numbers.
Here,

∴ 250 = 2 × 5 × 5 × 5
450 = 2 × 3 × 3 × 5 × 5
600 = 2 × 2 × 2 × 3 × 5 × 5
∴ HCF = 2 × 5 × 5 = 50
∴ The greatest number is 50.
Example 3: Find the greatest number which
divides 42, 53 and 67 leaving remainders 6, 5 and 7 respectively.
Solution:
Here, we should subtract the
remainders from the corresponding numbers,
42 – 6 = 36
53 – 5 = 48
67 – 7 = 60
Now the HCF of 36, 48 and 60 the
required greatest number.
Here,

∴ 36
= 2 × 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
60 = 2 × 2 × 3 × 5
∴ HCF = 2 × 2 × 3 = 12
∴ The greatest number is 12.
Do you have any problem regarding HCF (Highest Common Factor)?
You can comment your questions or problems here.




Great Post! Thanks a lot for publishing it.
ReplyDeleteamazing omg gyan article
ReplyDeleteThanking You One Of The Best article
ReplyDelete