Exponential Equation

Exponential Equation

An equation which contains the unknown variable appearing as an exponent of a base is known as an exponential equation. In the equation 5^x = 25, the unknown variable x is an exponent of base 5. So this equation is called an exponential equation.

********************

10 Math Problems officially announces the release of Quick Math Solver, an Android App on the Google Play Store for students around the world.

********************

The axioms given below help to solve the exponential equations:

a)    If x^a = y^a, then x = y

b)   If x^a=x^b, then a = b

c)    If x^a = 1, then x^a = x⁰. So a = 0

The following steps are useful to solve the exponential equation:

1.    Simplify both sides of the equation

2.    Make both sides of the equation into the same base.

3.    Equate their exponents and simplify.

Workout Examples

Solution: Here,

          a)      2^x+4 = 8^x

          or,     2^x+4 = (2³)^x

          or,     2^x+4 = 2^3x

          ∴        x+4 = 3x

          or,     4 = 3x – x

          or,     4 = 2x

          or,     x = 4/2

          or,     x = 2 

      

           

Example 3: Solve: 3^2x+1 – 9^x+1 + 54 = 0

Solution: Here,

                   3^2x+1 – 9^x+1 + 54 = 0

          or,     3^2x.3¹ – 9^x.9¹ = -54

          or,     9^x.3 – 9^x.9 = -54

          or,     9^x(3 – 9) = -54

          or,     9^x.-6 = -54

          or,     9^x = -54/-6

          or,     9^x = 9

          or,     9^x = 9¹

          ∴        x = 1

 

 

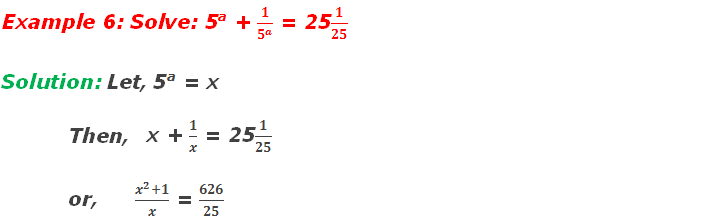
or,     25x² + 25 = 626x

or,     25x² – 626x + 25 = 0

or,     25x² – 625x – x + 25 = 0

or,     25x(x – 25) – 1(x – 25) = 0

or,     (x – 25)(25x – 1) = 0

∴ Either, x – 25 = 0

          or, x = 25

          or, 5^a = 52

          ∴ a = 2

Or, 25x – 1 = 0

          or, 25x = 1

          or, x = 1/25

          or, x = 1/5²

          or, 5^a = 5^-2

          ∴ a = -2

∴ a = 2 or -2

 

Example 7: Solve: 4 × 3^x+1 = 27 + 9^x

Solution: Here,

                   4 × 3^x+1 = 27 + 9^x

          or,     9^x – 4 × 3^x+1 + 27 = 0

          or,     3^2x – 4 . 3^x . 3¹ + 27 = 0

          or,     (3^x)² – 12 . 3^x + 27 = 0

          Let, 3^x = a

          Then, a² – 12a + 27 = 0

          or,     a² – 9a – 3a + 27 = 0

          or,     a(a – 9) -3(a – 9) = 0

          or,     (a – 9)(a – 3) = 0

∴ Either, a – 9 = 0

          or, a = 9

          or, 3^x = 3²

          ∴ x = 2

Or, a – 3 = 0

          or, a = 3

          or, 3^x = 3¹

          ∴ x = 1

∴ x = 1 or 2

 

You can comment your questions or problems regarding the exponential equations here.