LCM of Algebraic Expressions

8 comments

LCM of Algebraic Expressions


LCM of Algebraic Expressions

 

To calculate the LCM (Lowest Common Multiple) of the given algebraic expressions, we should convert the algebraic expressions into their simplest factors. And, then the product of their common factors and the remaining factors will give the LCM of the given algebraic expressions.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************



∴ LCM = Common factors × Remaining factors

 

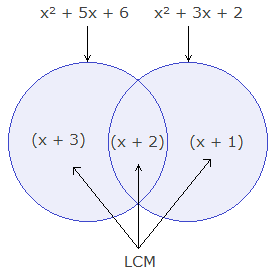
For example: x2 + 5x + 6 and x2 + 3x + 2 are two algenraic expressions. x2 + 5x + 6 = (x + 2)(x + 3) and x2 + 3x + 2 = (x + 1)(x+2) are their simplest factors.  And, (x + 1)(x + 2)(x + 3) is the product of their common and remaining factors. So, LCM of x2 + 5x + 6 and x2 + 3x + 2 is (x + 1)(x + 2)(x + 3).

 

LCM in Venn diagram


While finding LCM, we should use the following steps:


Steps:

                                                                  

1.     Factorize the given algebraic expressions.

2.     Take out the common factors and then the remaining factors.

3.     The product of common and remaining factors will give the required LCM.

 

The concept of LCM will be more clear from the following worked-out examples.


Worked Out Examples

 

Example 1: Find the LCM of 3x2yz, 4y2z and 5xz2

 

Solution:

 

Here,

 

1st expression = 3x2yz = 3 × x × x × y × z

 

2nd expression = 4y2z = 2 × 2 × y × y × z

 

3rd expression = 5xz2 = 5 × x × z × z

 

∴ LCM = 3 × 2 × 2 × 5 × x × x × y × y × z × z

             = 60x2y2z2 



Example 2: Find the LCM of m4 – 4m2 and 3m2 + 6m

 

Solution: 


Here,

 

1st expression = m4 – 4m2

                          = m2(m2 – 4)

                          = m2(m2 – 22)

                          = m × m(m + 2)(m – 2)

 

2nd expression = 3m2 + 6m

                           = 3m(m + 2)

 

∴ LCM = 3m × m(m + 2)(m – 2)

             = 3m2(m + 2)(m – 2)

 

 

Example 3: Find the LCM of a2 – 3a + 2, a4 + a3 – 6a2 and a3 + 2a2 – 3a

 

Solution:

 

Here,

 

1st expression = a2 – 3a + 2

                          = a2 – (2 + 1)a + 2

                          = a2 – 2a – a + 2

                          = a(a – 2) – 1(a – 2)

                          = (a – 2)(a – 1)

 

2nd expression = a4 + a3 – 6a2

                           = a2(a2 + a – 6)

                           = a2{a2 + (3 – 2)a – 6}

                           = a2(a2 + 3a – 2a – 6)

                           = a2{a(a + 3) – 2(a + 3)}

                           = a × a(a + 3)(a – 2)

 

3rd expression = a3 + 2a2 – 3a

                          = a(a2 + 2a – 3)

                          = a{a2 + (3 – 1)a – 3}

                          = a(a2 + 3a – a – 3)

                          = a{a(a + 3) – 1(a + 3)}

                          = a(a + 3)(a – 1)

 

∴ LCM = a × a(a – 1)(a – 2)(a + 3)

             = a2(a – 1)(a – 2)(a + 3)



Example 4: Find the LCM of x2 – 5x + 6, x2 + 4x – 12 and x2 – 2x

 

Solution:

 

Here,

 

1st expression = x2 – 5x + 6

                          = x2 – (3 + 2)x + 6

                          = x2 – 3x – 2x + 6

                          = x(x – 3) – 2(x – 3)

                          = (x – 3)(x – 2)

 

2nd expression = x2 + 4x – 12

                           = x2 + (6 – 2)x – 12

                           = x2 + 6x – 2x - 12

                           = x(x + 6) – 2(x + 6)

                           = (x + 6)(x – 2)

           

3rd expression = x2 – 2x

                          = x(x – 2)

 

∴ LCM = x(x – 2)(x – 3)(x + 6)

 

 

Example 5: Find the LCM of a2 – b2 – 2bc – c2, b2 – c2 – 2ca – a2 and c2 – a2 – 2ab – b2

 

Solution:

 

Here,

 

1st expression = a2 – b2 – 2bc – c2

                          = a2 – (b2 + 2bc + c2)

                          = a2 – (b + c)2

                          = (a + b + c)(a – b – c)

 

2nd expression = b2 – c2 – 2ca – a2

                           = b2 – (c2 + 2ca + a2)

                           = b2 – (c + a)2

                           = (b + c + a)(b – c – a)

                           = (a + b + c)(b – c – a)

           

3rd expression = c2 – a2 – 2ab – b2

                           = c2 – (a2 + 2ab + b2)

                           = c2 – (a + b)2

                           = (c + a + b)(c – a – b)

                           = (a + b + c)(c – a – b)

 

∴ LCM = (a + b + c)(a – b – c)(b – c – a)(c – a – b)



Example 6: Find the LCM of a3 – 2a2b + 2ab2 – b3, a4 + b4 + a2b2 and 4a4b + 4ab4

 

Solution:

 

Here,

 

1st expression = a3 – 2a2b + 2ab2 – b3

                          = a3 – b3 – 2a2b + 2ab2

                          = (a – b)(a2 + ab + b2) – 2ab(a – b)

                          = (a – b)(a2 + ab + b2 – 2ab)

                          = (a – b)(a2 – ab + b2)

 

2nd expression = a4 + b4 + a2b2

                           = (a2)2 + 2a2b2 + (b2)2 – a2b2

                           = (a2 + b2)2 –(ab)2

                           = (a2 + b2 + ab)(a2 + b2 – ab)

                           = (a2 + ab + b2)(a2 – ab + b2)

           

3rd expression = 4a4b + 4ab4

                           = 4ab(a3 + b3)

                           = 4ab(a + b)(a2 – ab + b2)

∴ LCM = 4ab(a + b)(a – b)(a2 + ab + b2)(a2 – ab + b2)



Example 7: Find the LCM of a2 – 18a – 19 + 20b – b2, a2 + a – b2 + b and 4a2 – 4b2 + 8b - 4

 

Solution:

 

Here,

 

1st expression = a2 – 2.a.9 + 92 – 100 + 20b – b2

                          = (a – 9)2 – (102 – 2.10.b + b2)

                          = (a – 9)2 – (10 – b)2

                          = {(a – 9) + (10 – b)}{(a – 9) – (10 – b)}

                          = (a – 9 + 10 – b)(a – 9 – 10 + b)

                          = (a – b + 1)(a + b – 19)

 

2nd expression = a2 + a – b2 + b

                           = a2 – b2 + a + b

                           = (a + b)(a – b) + 1(a + b)

                           = (a + b)(a – b + 1)

 

3rd expression = 4a2 – 4b2 + 8b - 4

                           = 4(a2 – b2 + 2b – 1)

                           = 4{a2 – (b2 – 2b + 1)}

                           = 4{a2 – (b – 1)2}

                           = 4(a + b – 1)(a – b + 1)

 

∴ LCM = 4(a + b)(a + b – 1)(a – b + 1)(a + b – 19)



Example 8: Find the LCM of 1 + 4a + 4a2 – 16a4, 1 + 2a – 8a3 – 16a4 and 1 – 8a3

 

Solution:

 

Here,

 

1st expression = 1 + 4a + 4a2 – 16a4

                          = 12 + 2.1.2a + (2a)2 – (4a2)2

                          = (1 + 2a)2 – (4a2)2

                          = (1 + 2a + 4a2)(1 + 2a – 4a2)

 

2nd expression = 1 + 2a – 8a3 – 16a4

                           = 1(1 + 2a) – 8a3(1 + 2a)

                           = (1 + 2a)(1 – 8a3)

                           = (1 + 2a){13 – (2a)3}

                           = (1 + 2a)(1 – 2a)(1 + 2a + 4a2)

 

3rd expression = 1 – 8a3

                           = 13 – (2a)3

                           = (1 – 2a)(1 + 2a + 4a2)

 

∴ LCM = (1 + 2a)(1 – 2a)(1 + 2a + 4a2)(1 + 2a – 4a2)

 

If you have any question or problems regarding the LCM of algebraic expressions, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…

Labels:

About author: Min Rajbanshi

I am a school math teacher and a blogger since 2012. I do blogging on a variety of topics including math. Over the years, I've explored and written about a wide range of topics, with a particular emphasis on mathematics. My passion for education extends beyond the classroom, as I enjoy sharing knowledge and insights on various subjects through my blog.

8 comments:

  1. UnknownSeptember 7, 2021 at 12:28 AM

    Helpful.

    ReplyDelete
  2. UnknownNovember 13, 2021 at 3:15 AM

    find lcm of a^3+1,a^6-1 and a^4+a^2+1

    ReplyDelete
    Replies
    1. Min RajbanshiNovember 13, 2021 at 4:27 PM

      Here is the solution to your problems,
      [image src="https://blogger.googleusercontent.com/img/a/AVvXsEj2V9lvn0R0YdCO96GEkq5WGxRKDMBEaQdhjtXhks_Tgz5hieIFEFQeizjK2EzwDYoTQrvGSSx0vuZB4P9d5tUDvuxumEOcEMMMdRmtDKJIqM-G0wr7A10nzYwWqbYCkRYUPbe7pzVGRaOLw5fC18XuK3rZAxve7v4QZIwMRTzSLIDzISe5UA5Kub-PNg=s16000 "/]

      You can solve it by yourself using Quick Math Solver. Please install the app by using the link given above. If you have more problems, post it here.

      Delete
  3. UnknownJanuary 20, 2022 at 5:10 PM

    LCM of
    a^4 + 4b^4 + (a² + b²)5b²,
    a² + 2a³b + a²b² -9b^4

    ReplyDelete
    Replies
    1. Min RajbanshiJanuary 21, 2022 at 12:12 AM

      Here is the solution to your problem,
      [image src="https://blogger.googleusercontent.com/img/a/AVvXsEj66k6Nsbh5CJ6fzfFgXhX1ceXvih-f0-dy_I5NZBV4JFcnjXSM-ghr9tSbfPlYs_yivB2VXWecTgnE7cp6DW79gS477rEb1MTg85aD6ZM_8yeQVtt6y4Bq7DmZTFNng7n_TwQeCjKwMYFynHSoYSCPXApD3AQUpzZx2KcjV1mI9Qx9FnoNJdzaMriSsA=s16000"/]

      Delete
  4. mohsinFebruary 20, 2022 at 2:44 AM

    Very efficiently written information. It will be beneficial to anybody who utilizes it, including me. Keep up the good work. For sure i will check out more posts. This site seems to get a good amount of visitors. Quantitative Reasoning Math

    ReplyDelete
  5. UnknownMarch 11, 2022 at 9:43 AM

    Factorization of 4a^3-16a^2+20a-8
    4acube +16 a square +20a -8

    ReplyDelete
    Replies
    1. Min RajbanshiMarch 12, 2022 at 7:04 AM

      You can solve it by using our app Quick Math Solver. Please Install it on your android phone.
      Here is the solution to your problems,
      [image src="https://blogger.googleusercontent.com/img/a/AVvXsEiYYqmMVjVaUPQXStu_b5-FS4LVLvX-iiHY3g7yQtW6MVF72RhlGpT_Z05oHFG5Eb_VNt8HA64qLAe1cjT1ruwi-R5dvSCmqj8rWajsS4M_FvhGd-5k9u5UQJZyYBxXxEfLzaquWY6kiRWQYKZdyFXz6j8rTJJn1oDvzQ0YZuE8GAmyd0utvzlarMdtRA=s16000"/]

      Delete

Subscribe to: Post Comments (Atom)