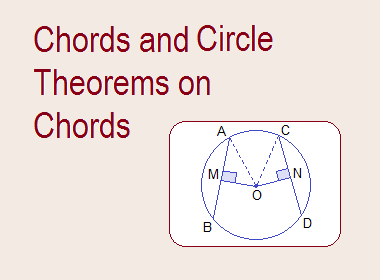
Chords and Circle Theorems on Chords
The line segment joining any two points on the
circumference of a circle is called the chord of the circle. In the figure given below: AB,
CD and EF are the chords. AB is also the diameter. Diameter is the longest
chord.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Circle Theorems on Chords
1.
In a circle, a perpendicular from the centre to its chord, bisect the chord.
2.
Equal chords of a circle are equidistant
from the centre of the circle.
Proofs:
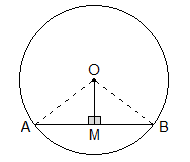
1. In a circle, a perpendicular from the centre to its chord, bisect the chord.
Given: O is the centre of
circle and OM is perpendicular to chord AB.
To
Prove:
AM = BM
Construction: OA and OB are joined.
Proof:
Statements Reasons
1.
In DAOM
and DBOM
i. ∠AMO = ∠BMO
(R) --------> Both are right angles; OM⊥AB
ii. OA
= OB (H) --------------> Radii of the same circle
iii. OM
= OM (S) --------------> Common side
2.
DAOM ≅DBOM
-----------------> By RHS axiom
3.
AM = BM ----------------->
Corresponding sides of congruent triangles.
Proved.
Note: The converse of this theorem i.e. “A straight line joining the centre of circle and
mid-point of a chord is perpendicular to the chord.” is also true.
2. Equal chords
of a circle are equidistant from the centre of the circle.
Given: O is the centre of the circle, chord AB = chord CD. OM⊥AB and ON⊥CD.
To
Prove:
OM = ON
Construction: OA and OC are joined.
Proof:
Statements Reasons
1.
AM = AB/2 and CN = CD/2 --->
Perpendicular from centre to chord bisect it.
2.
AB = CD ---------------------> By given
3.
AM = CN --------------------> From
statements 1 and 2
4.
In DAMO
and DCNO
i. ∠AMO = ∠CNO
(R) ---------> Both are right angles
ii. OA
= OC (H) ---------------> Radii of the same circle
iii. AM
= CN (S) ---------------> From statement 3.
5.
DAMO ≅DCNO
------------------> By RHS axiom
6.
OM = ON ----------------->
Corresponding sides of congruent triangles.
Proved.
Note: The converse of this theorem i.e. “Chords which are at equidistant from the centre of a circle are equal in length.” is also true.
Look at the following worked out examples:
Workout Examples
Example 1: In the figure, O is the centre of the circle and OM⊥AB. If OP = 10cm and OM = 6cm, find the length of the chord AB.
Solution: In the figure,
OP = 10cm
OA = 10cm [∵ Radii of same circle]
OM = 6cm
Now,
AB = 2 × AM [∵
Perpendicular bisects the chord]
= 2 ×
8cm
= 16cm
Example 2: In the figure, O is the centre of the circle, chord AB =
6cm, chord CD = 12cm, OM⊥CD and ON⊥AB. Find the distance between the chords
if the radius is 3√5cm.
Solution: In the figure,
OP = OC = 3√5cm
CM = CD/2 = 12/2 = 6cm
AN = AB/2 = 6/2 = 3cm
Now,
MN = ON - OM
= 6 –
3 cm
= 3cm
∴ The distance between chords is 3cm.
Example 3: In the fugure O is the centre of the circle and DABC ≅ DDBC. Prove that OM is the bisector of ∠AMD.
Solution:
Given:
In the figure O is the centre of the circle and DABC
≅ DDBC.
To Prove:
OM is the bisector of ∠AMD.
Construction: OP⊥AC and OQ⊥BD are drawn.
Proof:
Statements Reasons
1. AC = BD ---------> Corresponding
sides of ≅ Ds
ABC and BCD
2. OP = OQ --------> Equal chords of
a circle are equidistant from the centre.
3. In DOPM and DOQM
i. ∠OPM = ∠OQM (R) ---------> Both are right angles
ii. OM
= OM (H) ----------> Common side
iii. OP
= OQ (S) -----------> From statement 2
4. DOPM
≅ DOQM
-------------> By RHS axiom
5. ∠PMO
= ∠QMO
i.e.
∠AMO
= ∠DMO
------------> Corresponding angles of ≅ triangles.
6. OM
is the bisector of ∠AMD --------------> From
statement 5.
Proved.
Example 4: In the fugure O is the centre of the circle and PM = QN.
Prove that DPOQ is an isosceles triangle.
Solution:
Given:
O is the centre of the circle and PM = QN.
To Prove:
DPOQ is an isosceles triangle.
Construction: OM and ON are joined.
Proof:
Statements Reasons
1.
∠OMN = ∠ONM --------> Base angles of an isosceles DOMN (OM = ON)
2.
∠OMP = ∠ONQ --------> Supplementary angles of equal angles ∠OMN = ∠ONM (Statement 1)
3.
In
DOMP and DONQ
i. OM
= ON (S) ---------> Radii of same circle
ii. ∠OMP = ∠ONQ (A) ----------> From statement 2
iii. PM
= QN (S) -----------> By given
4.
DOMP
≅ DONQ -------------> By SAS axiom
5.
OP = OQ -------------> Corresponding sides of ≅ triangles.
6.
DPOQ
is an isosceles triangle --------> From statement 5.
Proved.
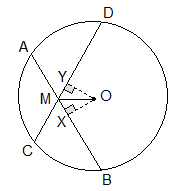
Example 5: In the fugure, chords AB and CD intersect at M. If OM is
the bisector of ∠BMD, prove that AB = CD.
Solution:
Given:
OM is the bisector of ∠BMD.
To Prove:
AB = CD.
Construction: OX⊥AB and OY⊥CD are drawn.
Proof:
Statements Reasons
1. In DOMX and DOMY
i. OM
= OM (S) ---------> Common side
ii. ∠OMX = ∠OMY (A) -------> Being OM a bisector of ∠BMD (given)
iii. ∠MXO = ∠MYO (A) -------> Both right angles.
2. DOMX
≅ DOMY -------------> By SAA axiom
3. OX
= OY -------------> Corresponding sides of ≅ triangles.
4. AB = CD
------> Chords equidistant from centre of a circle are equal.
Proved.
You can comment your questions or problems regarding chords and circle theorems on chords here.








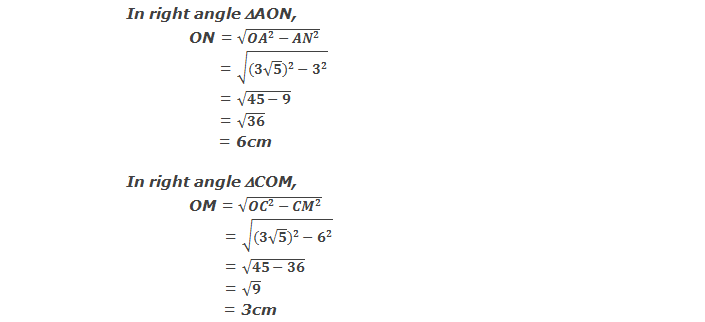


0 comments: