
Central Angles and Inscribed Angles
The angle formed at the centre of a circle is called a central angle and the angle formed at the circumference of a circle is called a circumference angle or inscribed angle.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************

To understand and prove the circle theorems on central angles and inscribed angles, we use the following axioms on arcs and angles subtended by them:
1.
Degree measurement of a full circle arc is equivalent to 360°.
2.
Central angle of a circle is equal to the degree measurement of
It's opposite arc.
3.
Inscribed angle of a circle is equal to half of the degree
measurement of its opposite arc.
Theorems:
1. Central angle of a
circle is double of inscribed angle standing on the same arc.
2. The angles at the
circumference of a circle standing on the same arc are equal.
3. Inscribed angle on a semi-circle is a right angle.
Proofs:
1. Central angle of a circle is double of inscribed angle standing on the same arc.

Given: O is the centre of
a circle. ∠AOB is a central angle and ∠ACB is
an inscribed angle standing on the same arc AB.
To Prove: ∠AOB = 2∠ACB
Proof:
Statements Reasons
1.
∠AOB = Arc AB ----> Central angle is equal to its opposite
arc.
2.
∠ACB = ½ Arc AB ---->
Inscribed angle is equal to half of its opposite arc.
3.
2∠ACB = Arc AB -----> From statements 2.
4. ∠AOB = 2∠ACB -----> From statements 1 and 2.
Proved.
2. The angles at the circumference of a circle standing on the same arc are equal.

Given: O is the centre of
a circle. ∠ABC and ∠ADC are the inscribed angles standing on same
arc AC.
To Prove: ∠ABC = ∠ADC
Proof:
Statements Reasons
1.
∠ABC = ½ Arc AC ----> Inscribed angle is equal to the half of
It's opposite arc.
2.
∠ADC = ½ Arc AC ----> Inscribed angle is equal to the half of its opposite
arc.
3.
∠AOB = 2∠ACB -----> From statements 1 and 2.
Proved.
3. Inscribed angle on a semi-circle is a right angle.

Given: O is the centre of
a circle. AB is a diameter.
To Prove: ∠ACB = 90°
Proof:
Statements Reasons
1.
∠AOB = 180° ------> Being ∠AOB a straight angle.
2.
∠ACB = ½ ∠AOB ---> Inscribed angle is equal to the half of its opposite
arc.
3.
∠ACB = ½ × 180° ---> From statements 1 and 2.
4.
∠ACB = 90° -------> From statement 3.
Proved.
Worked Out Examples:
Example 1: Find the value of x and y in the given figure.

Solution:
From the figure,
∠OCA
= ∠OAC
= 50° [Being OA = OC, Radii of same circle]
y + 50° + 50° = 180° [Sum of the
angels of DOAC]
or, y
+ 100° = 180°
or, y
= 180° - 100°
or, y
= 80°
Now,
x = ½ of y [Inscribed angle is
half of central angle]
= ½ × 80°
=
40°
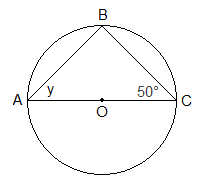
Example 2: Find the value of y in the given figure.
Solution:
From the figure,
∠ABC = 90°
[An angle formed on semi-circle]
y + 50° + 90° = 180° [Sum of the
angles of DABC]
or, y
+ 140° = 180°
or, y
= 180° - 140°
= 40°
Example 3: Find the value of z in the given figure.
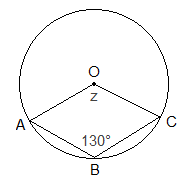
Solution:
From the figure,
Reflex ∠AOC = 2∠ABC [Central angle is double of
inscribed angle on the same arc]
= 2 × 130°
= 260°
Now,
z + reflex ∠AOC = 360° [Angles at one complete
rotation]
or, z
+ 260° = 360°
or, z
= 360° - 260°
or, z = 100°
Example 4: What is the size of ∠CBX in the given figure?

Solution:
From the figure,
∠ADB
= 32° and ∠BXC
= 85°
∠ACB
= ∠ADB = 32°
[Inscribed angles on same arc]
Now,
∠CBX
+ ∠ACB
+ ∠BXC =
180° [Sum of angles of DBXC]
or, ∠CBX + 32° + 85° = 180°
or, ∠CBX + 117°= 180°
or, ∠CBX = 180° - 117°
or, ∠CBX = 63°
Example 5: In the given diagram, PQR is an isosceles triangle with PQ = PR and a circle is drawn with PQ as a diameter. Prove that QS = RS.

Solution:
Given: In ΔPQR, PQ = PR. O is centre and PQ is a
diameter of circle.
To Prove: QS = RS.
Construction: Points P and S are joined.
Proof:
Statements Reasons
1. ∠PSQ = 90° ----> Being ∠PSQ is in
semi-circle with diameter PQ
2.
In ΔPSQ and ΔPSR
i. ∠PSQ = ∠PSR (R) ----> Each of 90°
(Statement 1)
ii. PQ = PR (H) -----> By given
iii. PS = PS (S) -----> Common side.
3.
ΔPSQ ≅ ΔPSR -------> By RHS axiom
4.
QS = RS ------> Corresponding
sides of ≅ triangles.
Proved.
Example 6: In the given figure, O is the centre of the circle, PQ the diameter and AO⊥PQ, prove that ∠PBR = ∠PAO.
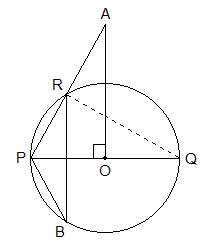
Solution:
Given: PQ is the diameter of a circle with centre at O and
AP⊥PQ.
To Prove: ∠PBR = ∠PAO.
Construction: Points R and Q are joined.
Proof:
Statements Reasons
1. ∠PRQ = 90° ----> Being ∠PRQ is in
semi-circle with diameter PQ
2.
In ΔPQR and ΔPAO
a)
∠PRQ = ∠PAO ----> Being AP⊥PQ, and from statement 1.
b)
∠QPR = ∠APO ----> Common angle.
c)
∠PQR ∠PAO ---->
Remaining angles.
3.
∠PQR = ∠PBR -----> Being inscribed angles on same arc PR.
4.
∠PBR = ∠PAO ----> From statements 1(c) and 3.
Proved.
Example 7: In the given figure, O is the centre of the circle, AB the diameter and arc BC = arc CD. Prove that AD || OC.

Solution:
Given: O is the centre of circle. AB is the diameter. Arc
BC = arc CD
To Prove: AD || OC.
Proof:
Statements Reasons
1. ∠BAD = ½ of arc BCD ---> Inscribed angle is equal to the half of its
opposite arc
2.
∠BAD = ½ of arc (BC + CD) ---> whole
part axiom from statement 1
3.
∠BAD = ½ of arc (BC + BC) --->
Being arc BC = arc CD (given).
4.
∠BAD = ½ × arc 2BC ---> From statements 3.
5.
∠BAD = arc BC ---> From statement 4.
6.
∠BOC = arc BC ---> Central angle is
equal to its opposite arc.
7.
∠BAD = ∠BOC ---> From statements 5 and 6.
8.
AD // OC ---> Being corresponding
angles equal (statement 7)
Proved.
Do You Have Any Questions regarding the circle theorems?
You can ask your questions or problems here in the comment section below.



Very helpful.
ReplyDelete