Probability
The dictionary meaning of the word
‘probability’ is ‘likely though not certain to occur’. Thus when a coin is
tossed a head is likely to occur but it may not occur. Here, the probability of
occurrence of head or tail is ½ and it is also called 50/50 chance.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Probability is a concept that numerically measures the degree
of certainty and therefore of uncertainty of the occurrence of events.
Definitions of basic terms on probability
There are some basic terms which are
frequently used in probability. It is essentially important to have the proper
concept of these terms.
1. Random experiments:
Any experiment whose
outcome cannot be predicated or determined in advance is called a random
experiment. Tossing a coin, rolling a dice, drawing a card from a well shuffled
pack of 52 playing cards etc. are a few examples of random experiments.
2. Outcomes:
The results of a random
experiment are called outcomes or events. For example, while tossing a coin,
the occurrence of head or tail is the outcome.
3. Sample space:
Each performance in a
random experiment is called a trial and an outcome of a trial is called a
sample point. The set of all possible outcomes (i.e. sample points) of a random
experiment is known as sample space. Usually a sample space is denoted by S.
For example,
i. The possible outcomes of a
random experiment of throwing a dice are 1, 2, 3, 4, 5 or 6.
∴ The sample space, S = {1, 2,
3, 4, 5, 6}
ii. The possible outcomes of a
random experiment of tossing a coin are head (H) or tail (T).
∴ The sample space, S = {H, T}
iii. When two coins are tossed
simultaneously, the sample space, S = {HH, HT, TH, TT}
4. Event:
A sample space S of a
random experiment is a universal set. Every non-empty subset of the sample
space S is called an event. For example, while tossing a coin, the sample
space, S = {H, T}.
Here, the subsets {H},
{T} and {H, T} are the events of S. The empty set φ is also an event of S, but
it is the ‘impossible event’. S is called the ‘sure event’. An event containing
only one element of S is called a simple or elementary event. For example,
If S = {H, T}, then {H}
and {T} are the elementary events.
If S = {1, 2, 3, 4, 5,
6}, then {1}, {2}, {3}, {4}, {5} and {6} are the elementary events.
5. Exhaustive cases:
The total number of all
possible outcomes of a random experiment is known as exhaustive cases. For
example,
While tossing a coin, S
= {H, T}
So, exhaustive cases = 2
While tossing two coins
simultaneously, S = {HH, HT, TH, TT}
So, exhaustive cases = 4
While throwing a dice, S
= {1, 2, 3, 4, 5, 6}
So, exhaustive cases = 6
6. Favourable and
unfavourable cases:
The outcomes in an
random experiment which are desirable (expected) to us are called favourable
cases and all ther cases are unfavourable cases. For example:
While tossing a coin, S
= {H, T}
Here, the favourable
number of cases of head is 1 and tail is also 1.
While tossing two coins,
S = {HH, HT, TH, TT}
The favourable number of
cases of both of them head is 1 and tail is also 1. The favourable number of cases
of at least one head is 3 and at least one tail is also 3.
7. Equally likely events:
Two or more events are
said to be equally likely if the chance of occurring any one event is equal to
the chance of occurring other cases. For example, while throwing a dice, the
chance of coming up the numbers 1 to 6 is equal. Similarly, while tossing a coin,
head (H) or tail (T) are equally likely events.
8. Independent and
dependent events:
Two or more events are
said to be independent if the occurrence of one of the events does not affect
the occurrence of other events. For example, in the random experiment of
tossing a coin twice or more, the occurrence of any one event in the first
trial does not affect the occurrence of any event in the second trial.
On the other hand, two
or more events are said to be dependent if the occurrence of one of the events affects
the occurrence of the other events.
For example, while
drawing a ball in two successive trials from a bag containing 2 red and 3 green
without a replacement, getting any one coloured ball in the first trial affects
to draw another ball in the second trial. So these are the dependent events.
9. Mutually exclusive
events:
Two or more events of a
sample space S are said to be mutually exclusive if the occurrence of any one
event excludes the occurrence of the other events.
For example, while
tossing a coin, the occurrence of head excludes the occurrence of tail or vice
versa. So they are mutually exclusive events.
Furthermore, consider
the experiment of throwing a dice. Let A be the event, ‘the number obtained is
less than 5’. Then, A = {1, 2, 3, 4}. Again, B be the event, ‘the number
obtained is at least 5’. Then, B = {5, 6}. Here A∩B = φ.
Thus, the joint
occurrence of A and B is an impossible event. In this case the events A and B
are called mutually exclusive events. In general, if A and B are any two events
on a sample space S and A∩B = φ, the events A and B are
said to be mutually exclusive.
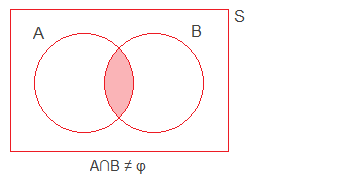
10. Non-mutually exclusive events:
If A and B are any two events on a sample space S and A∩B ≠ φ, the events are said to be non-mutually exclusive events.
For example, let’s
consider the experiment of throwing a dice. Let A be the event ‘the number
obtained is even’ and B be the event ‘the number obtained is less than 4’.
Then, A = {2, 4, 6} and B = {1, 2, 3} and ∴ A∩B = {2}. It means, ‘an even
number from 1 to 6’ and ‘a number less than 4’ can occur simultaneously in a
single throw of a dice. So A and B are said to be non-mutually exclusive
events.
Some useful terms related to playing cards, coin and dice:
Playing cards:
·
There are 52 cards in a
packed of playing cards.
·
There are 26 red and 26 black
coloured cards in a packet.
·
13 Hearts (♥) and 13 diamonds (♦) are the
red coloured cards.
·
13 Spade (♠) and 13 clubs (♣) are the black coloured
cards.
·
There are 1/1 heart and
diamond ace and 1/1 spade and club ace in a packet of playing cards.
·
There are 12 face cards in
the packet. Among them 4 are Jacks (heart, diamond, spade and club), 4 are
Queens and 4 are Kings.
Coin:
·
There are two faces of a
coin, head (H) and tail (T).
Dice:
·
There are six faces in a dice
which are numbered from 1 to 6.
Theoretical probability of an event:
Let n(S) be the total number of all
possible outcomes (Exhaustive number of cases) of an experiment and n(E) be the
favourable number of cases of the sample space S, then the theoretical probability
of happening the event (E) is defined as,
Also, the probability of non-happening of the
event is given by
P’(E) = 1 – P(E)
Empirical or experimental probability:
When a coin is tossed, theoretically the
probability of getting head is ½. The probability obtained in this way is
called theoretical probability. On the other hand, if a coin is tossed 20
times, theoretically the head should occur ½ × 20 = 10 times. However, in real
experiment it may not happen, i.e. the occurrence of head may be 6, 9, 11 or 15
or any number of times. The probability of any event which is estimated on the
basis of the number of actual experiments is known as empirical or experimental
probability.
If n(S) be the total number of times, an
experiment is repeated and n(E) be number of observed outcomes, then the
empirical probability is defined as,
Probability scale:
Probability is measured on a scale within
0 to 1. A probability of 0 means that there is no chance of an event happening.
A probability or 1 means that it is certain the event will happen.
In the adjoining spinner, the probability
of pointer to stop on red is ½. The probability of the pointer to stop on blue
is ¼. The probability of the pointer to stop on yellow is ¼. The probability of
the pointer to stop on black is 0, which means not possible. The probability of
the pointer to stop on red, blue or yellow is 1 which means a sure event.
Thus, probability always lies in between
0 to 1, but it can never be less than 0 and more than 1.
Worked out probability examples:
Example 1: Among the number cards numbered from 1 to 20, a card is
drawn at random. Find the probability of getting a card whose number is exactly
divisible by 5.
Solution:
Let S be the
sample space and A be the favourable event that the number is exactly divisible
by 5. Then,
S = {1,
2, 3, 4, ……….., 20}
∴ n(S) = 20
A = {5,
10, 15, 20}
∴ n(A) = 4
Now,
P(A) = n(A)/n(S) = 4/20 = 1/5
Hence, the
probability of getting the card whose number is exactly divisible by 5 is 1/5.
Example 2: A card is drawn at random from a well shuffled pack of 52
cards. Find the probability of getting a face card.
Solution:
Let S be the
sample space and F be the favourable event of getting a face card, then
n(S) =
52
n(F) =
12
Now,
P(F) =
n(F)/n(S) = 12/52 = 3/13
Hence, the
probability of getting a face card is 3/13.
Example 3: A bag contains a dozen of identical ball pens, out of
which 5 are red colour and 7 are black colour. If a ball pen is taken out from
the bag randomly, find the probability that it is of red colour.
Solution:
Let S be the
sample space. R and B be the favourable events of getting red and black ball
pens respectively. Then,
n(R) = 5
n(B) = 7
n(S) =
5+7 = 12
Now,
P(R) =
n(R)/n(S) = 5/12
Hence, the
probability of getting red ball pen is 5/12.
Example 4: What is the probability that Nisha celebrates her
birthday on Tuesday?
Solution:
There are 7
days in a week. The birthday of a person must be one of these 7 days. Let S be
the sample space and T be the favourable event that she celebrates her birthday
on Tuesday. Then,
n(S) = 7
n(T) = 1
[∵ there is only one
Tuesday in a week.]
Now,
P(T) =
n(T)/n(S) = 1/7
Hence, the
probability of celebrating her birthday on Tuesday is 1/7.
Example 5: What is the probability that a leap year selected at
random has 53 Saturdays.
Solution:
The total
number of days in a leap year is 366 and also there are 7 days in a week.
Now,
366 ÷ 7 = 52+2/7
Clearly we
can see that all the days of a week appear 52 times and remaining 2 days may
appear as: {(Sun, Mon), (Mon, Tue), (Tue, Wed), (Wed, Thu), (Thu, Fri), (Fri,
Sat), (Sat, Sun)}. So there are 7 exhaustive cases and 2 favourable cases.
Let S be the
sample space and E be the favourable event of getting 53 Saturdays, then
n(S) = 7
n(E) = 2
Now,
P(E) =
n(E)/n(S) = 2/7
Hence, the
probability of 53 Saturdays in a leap year is 2/7.
Example 6: A circular plate has eight equal sectors numbered from 1
to 8 and a fixed arrow headed needle at the centre. If the plate is rotated,
find the probability that the needle will point at:
a)
2
b) Lucky number 7
c)
An odd number
d) A number greater than 5
Solution:
Let S be the
sample space. Then,
n(S) = 8
[∵ There are 8 sectors]
a)
Let, A be the favourable
event that the arrow points at 2, then
n(A) = 1
∴ P(A) = n(A)/n(S) = 1/8
b) Let, B be the favourable event that the arrow points at 7, then
n(B) = 1
∴ P(B) = n(B)/n(S) = 1/8
c)
Let, C be the favourable
event that the arrow points at an odd number, then
n(C) = 4
∴ P(C) = n(C)/n(S) = 4/8
= ½
d) Let, D be the favourable event that the arrow points at number
greater than 5, then
n(D) = 3
∴ P(D) = n(D)/n(S) = 3/8
Example 7: The given table represents the number of people of
different ages and sex in a live concert. If a person among them gets a car in
a lucky draw, find the probability that the person is:
a)
of age 16 to 24
b) male of age 25 to 40
c)
a female
d) not a female
Solution:
Here, the
total number of persons in the concert is
= 500 + 1500 + 1800 + 1200
= 5000
∴ n(S) = 5000
a)
Let, A be the favourable
event of the person being of age 16-24, then
n(A) = 500
+ 1800 = 2300
∴ P(A) = n(A)/n(S) = 2300/5000
= 23/50
b) Let, B be the favourable event of the person being male of age
25-40, then
n(B) = 1500
∴ P(B) = n(B)/n(S) = 1500/5000
= 3/10
c)
Let, F be the favourable
event of the person being a female, then
n(F) = 1800
+ 1200 = 3000
∴ P(F) = n(F)/n(S) = 3000/5000
= 3/5
d) Let, NF be the favourable event of the person not being a
female, then
P(NF) = 1
– P(F) = 1 – 3/5 = 2/5
Example 8: If a person having alcohol drives a vehicle, then the
probability of meeting an accident is 11/100. If an experiment is done where
1000 persons having alcohol drive vehicle, how many of them will:
a)
meet an accident
b) not meet an accident
Solution:
Let S be the
sample space and A be the favourable event of meeting an accident where 1000
persons having alcohol drive vehicle and the probability of meeting an accident
is 11/100. So,
n(S) = 1000
P(A) = 11/100
∵ P(A) = n(A)/n(S)
or, 11/100 = n(A)/1000
or, 100 × n(A) = 11000
or, n(A) = 11000/100
or, n(A) = 110
∴ 110 of them are likely to meet an accident and 1000-110 = 890
will not meet an accident.
Example 9: A cubical dice is thrown two times. Find the probability
that the outcomes are 6 in the first time and odd number in the second time.
Solution:
Here,
36 pairs can
be obtained as given in the table below.
So, n(S) = 36
The number
of pairs in which ‘6’ in the first and the odd number in the second are (6, 1),
(6, 3) and (6, 5), so n(S) = 3
We know,
P(A) =
n(A)/n(S) = 3/36 = 1/ 12
Example 10: Head occurs 10 times when a coin is tossed 25 times.
Find the empirical probability of tail.
Solution:
Let S be
the sample space i.e. total number of times an experiment is repeated and T be number
of events in which tail occurred. Then,
n(S) =
20 (total number of experiments)
n(T) = 25-10
= 15
Now,
P(T) =
n(T)/n(S) = 15/20 = 3/5
Hence, the empirical
probability of tail = 3/5.
You can comment your questions or problems regarding probability
here.












0 comments: