Trigonometry: Angles

Trigonometry: Angles

Trigonometry is a branch of mathematics dealing with the measurement of sides and angles of a triangle. We apply trigonometry in Engineering, Surveying, Astronomy, Geology etc.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

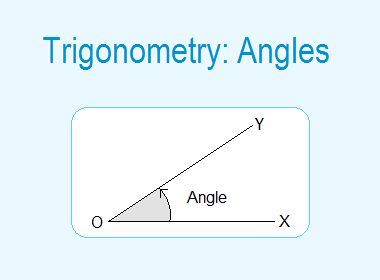
Angles:

Let O be the fixed point on OX, the initial line. Let OY be the revolving line. Then the amount of rotation of OY about O with respect to OX is known as the angle between OX and OY. Here the angle formed is ∠XOY.

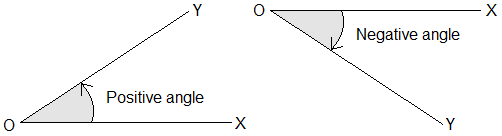
If the revolving line rotates about the fixed point O in the anticlockwise direction, the angle so formed is said to be positive.

If the revolving line rotates about the fixed point O in the clockwise direction, the angle formed is said to be negative.

Measurement of Angles

A line making one complete rotaion makes 360°. When a line makes a quarter tern, it makes 90° or 1 right angle. The size of a right angle is same in every measurement. The following three system are commonly used in the measurement of angles:

(a)  Sexagesimal System (Degree System)

(b) Centesimal System (Grade System)

(c)  Circular System (Radian System)

 

(a)  Sexagesimal System: This system is also called British System. In this system, the unit of measurement is degree. So, this system also is known as the degree system. In this system, a right angle is divided into 90 equal parts and each part is called a degree. A degree is divided into 60 equal parts and each part is called as one minute. A minute is also divided into 60 equal parts and each part is called as one second. Therefore, we have

60 seconds = 1 minute (60’’ = 1’)

60 minutes = 1 degree (60’ = 1°)

90 degrees = 1 right angle

                The degree, minute and second are denoted by (°), (’) and (’’) respectively.

 

(b) Centesimal System: This system is also called the French System. In this system, the unit of measurement is grade. So, this system also is known as the grade system. In this system, a right angle is divided into 100 equal parts and each part is called a grade. A grade is divided into 100 equal parts and each part is called a minute. A minute is also divided into 100 equal parts and each part is called a second. Therefore, we have

                          100 seconds = 1 minute (100’’ = 1’)

                          100 minutes = 1 grade (100’ = 1^g)

                          100 grades = 1 right angles

                 The grade, minute and second are denoted by (^g), (‘) and (‘’) respectively.

 

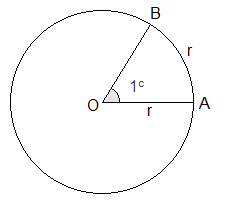
(c)  Circular System: In this system, the unit of measurement of an angle is a radian. An angle at the centre of a circle subtended by an arc equal to the length of radius of the circle is known as 1 radian. It is denoted by (^c). 

As the total length of circumference of a circle is 2πr units, the angle subtended by circumference of a circle at the centre is 2πr/r radian i.e. 2π^c.

                 Which is, 4 right angle = 2π^c

                 or,          1 right angle = (π/2)^c

 

Now, from the definition of sexagesimal measure, centicimal measure and circular measure of angles, we have,

                 1 right angle = 90° = 100^g = (π/2)^c

 

Theorem: “Radian is a constant angle.”

Proof:-

Let, O be the centre of the circle and OP = r be the radius of the circle. An arc PQ = r is taken. PO and QO are joined. Produce PO to meet circle at R. Then by definition ∠POQ = 1 radian. The diameter PR = 2r, ∠POR = 2 right angles = 180° and arc PQR = ½ × circumference = ½ × 2πr = πr.

Now, since the angles at the centre of a circle are proportional to the corresponding arcs on which the stand.

i.e.     ∠POQ/∠POR = arc PQ/arc PQR

or,      1 radian/180° = r/πr

or,      1 radian = (180/π)°

Since 1 radian is independent of the radius of the circle, it is a constant angle.

Proved.

Relation between different system of measurement of angles:

Since, 1 right angle = 90° and 1 right angle = 100^g

∴        90° = 100^g

∴        1° = (10/9)^g

Also,   1^g = (9/10)°

 

Again, π^c = 180° = 200^g

∴        1^c = (180/π)°          and    1^c = (200/π)^g

Also,   1° = (π/180)^c          and    1^g = (π/200)^c

Workout Examples

Example 1: Reduce 24^g 20’ 44’’ into centicimal seconds.

Solution:

          The given angle is 24^g 20’ 44’’

          = 24 × 100 × 100’’ + 20 × 100’’ + 44’’

          = 240000’’ + 2000’’ + 44’’

          = 242044’’

Example 2: Express 42° 20’ 15’’ into the number of degrees.

Solution:

          The given angle is 42° 20’ 15’’

          = 42° + (20/60)° + (15/60×60)°

          = 42° + 0.333333° + 0.004166°

          = 42.337499°

Example 3: Express 48^g 54’ 68’’ into degrees, minutes and seconds.

Solution:

          The given angle is 48^g 54’ 68’’

          = (48 + 54/100 + 68/100×100)^g

          = (48 + 0.54 + 0.0068)^g

          = 48.5468^g

          = (48.5468 × 9/10)°     [∵ 1^g = (9/10)°]

          = 43.69212°

          = 43° + 0.69212°

          = 43° + (0.69212 × 60)’

          = 43° + 41.5272’

          = 43° + 41’ + 0.5272’

          = 43° + 41’ + (0.5272 × 60)’’

          = 43° + 41’ + 31.632’’

          = 43° 41’ 31.63’’

Hence, 48^g 54’ 68’’ = 43° 41’ 31.63’’

 

Example 4: Express π/6 radians into sexagesimal and centicimal measures.

Solution:

          The given angle is π/6 radians

          = (π/6 × 180/π)°          [∵ 1^c = (180/π)°]

          = 30°

Again,

          π/6 radians

          = (π/6 × 200/π)^g           [∵ 1^c = (200/π)^g]

          = 33.33^g

 

Example 5: Reduce the following angles into radian measure.

a.    42^g75’

b.   42° 15’ 30’’

Solution:

a.    42^g 75’

          = (42 + 75/100)^g

          = (42 + 0.75)^g

          = 42.75^g

          = (42.75 × π/200)^c        [∵ 1^g = (π/200)^c]

          = 0.21375π^c

 

b.   42° 15’ 30’’    

= (42 + 15/60 + 30/60×60)°

= (42 + 0.25 + 0.00833)°

= 42.25833°

= (42.25833 × π/180)^c  [∵ 1° = (π/180)^c]

= 0.2348π^c

Example 6: The angles of a triangle are (7x/2)^g, (9x/4)° and (πx/50)^c. Find the angles of the triangle in degrees.

Solution: Here,

          First angle = (7x/2)^g = (7x/2 × 9/10)° = (63x/20)°

          Second angle = (9x/4)°

          Third angle = (πx/50)^c = (πx/50 × 180/π)° = (18x/5)°

Now, the sum of all angles of a triangle is 2 right angles.

i.e.     (63x/20)° + (9x/4)° + (18x/5)° = 180°

or,     {(63x + 45x + 72x)/20}° = 180°

or,     (180x/20)° = 180°

or,     (9x)° = 180°

or,     x° = 20°

Hence, the angles of the triangle are (63×20/20)°, (9×20/4)° and (18×20/5)° i.e 63°, 45° and 72°.

 

Example 7: Sum of the first and the second angle of a triangle is 150°. The ratio of the number of grades in the first angle to the number of degrees in the second angle is 5:3. Find the angles of the triangle in circular measure.

Solution: Suppose number of grades in the first angle be 5x and the number of degrees in the second angle be 3x.

          First angle = 5x^g = (5x × 9/10)° = (9x/2)°

          Second angle = 3x°

From question,

          9x/2 + 3x = 150°

or,     15x/2 = 150°

or,     15x = 300°

or,     x = 20°

∴        The first angle = 9x/2 = 9×20/2 = 90°

          The second angle = 3x = 3 × 20 = 60°

          The third angle = 180° - 150° = 30°

The angles of the triangle in circular measure are,

          (90 × π/180)^c, (60 × π/180)^c and (30 × π/180)^c

i.e.     (π/2)^c, (π/3)^c and (π/6)^c

 

You can comment your questions or problems regarding the system of measurement of angles here.