10 Math Problems: Matrix | What is Matrix?

Matrix | What is Matrix?

A matrix is a rectangular array of numbers arranged in horizontal and vertical lines and enclosed between round or square brackets. Horizontal lines are called rows and vertical lines are called columns of a matrix.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

Some examples of the matrix are given below:

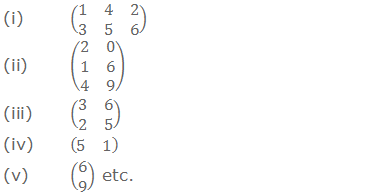
Each member or number in the array is called an element or an entry of the matrix. An element appearing in the i^th row and j^th column of a marix is called its (i, j)^th element or the (i, j)^th entry.

Order of a Matrix

The order or the size of the matrix is given by the number of rows followed by the number of columns. If a matrix contains m rows and n columns, then it is of order m × n, read as m by n.

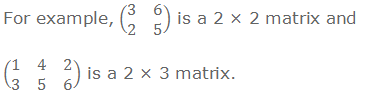
Matrix Notation

The matrices are usually denoted by capital letters such as A, B, C, ………etc. The elements are denoted by the corresponding small letters along with two suffixes. The first suffix indicates the number of row and latter one indicates the number of column in which the element appears.

a_ij is the element of a matrix A in the i_th row and j_th column.

a₂₃ is the element of a matrix A in the 2^nd row and 3^rd column.

Thus a matrix of order m × n may be written as

A = (a_ij)_{m × n}

If A is a 3 × 3 matrix, then it may be written as

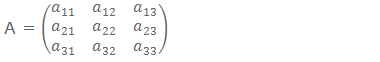
Types of Matrices

1. Row Matrix:

A matrix having only one row is called a row matrix. For example, (1 2 4) is a row matrix of order 1 × 3. Similarly (1 5), (3 -1 7 9) are row matrices of order 1 × 2 and 1 × 4 respectively.

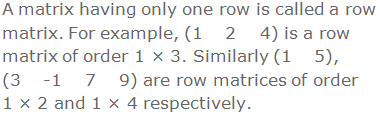
2. Column Matrix:

A matrix having only one column is called a column matrix. For example, the matrices (■(2@1)), (■(3@2@6)) and (█(2@9@3@7)) are column matrices of order 2 × 1, 3 × 1 and 4 × 1 respectively.

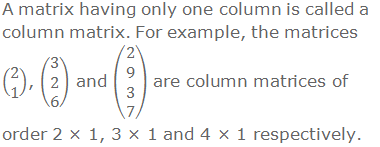
3. Square Matrix:

A matrix having same number of rows and columns is called a square matrix. For example, (■(1&2@3&4)) and (■(1&0&2@3&1&4@2&0&5)) are square matrices of order 2 × 2 and 3 × 3 respectively. A square matrix having order n × n is called a square matrix of order n. Thus the matrices given above are of order 2 and 3 respectively.

4. Rectangular Matrix:

A matrix in which the number of rows is not equal to the number of columns is called a rectangular matrix. For example, the matrices (■(1&2&3@4&0&5)) and (■(1&7@2&0@4&9)) are rectangular matrices of order 2 × 3 and 3 × 2 respectively.

5. Zero Matrix or Null Matrix:

If each element of a matrix is zero, then the matrix is called zero matrix or null metrix. For example, the matrices (■(0&0@0&0)), (■(0&0&0@0&0&0)) and (■(0&0&0@0&0&0@0&0&0)) are zero matrices of order 2 × 2, 2 × 3 and 3 × 3 respectively. Zero matrix is denoted by letter O.

6. Diagonal Matrix:

In a square matrix, the diagonal from the left top to the right bottom is called principal or leading diagonal, and all the elements in it are called diagonal elements. A square matrix having all non-diagonal elements zero is called a diagonal matrix. For example, the matrices (■(1&0@0&2)) and (■(1&0&0@0&2&0@0&0&3)) are diagonal matrices of order 2 and 3 respectively.

7. Scalar Matrix:

If all the diagonal elements of a diagonal matrix are same, then the matrix is called a scalar matrix. For example, the matrices (■(5&0@0&5)) and (■(-2&0&0@0&-2&0@0&0&-2)) are scalar matrices of order 2 and 3 respectively. [Note that a scalar matrix is a particular case of a diagonal matrix.]

8. Unit Matrix or Identity Matrix:

If all the diagonal elements of a diagonal matrix are unity, then the matrix is called an identity or unit matrix. For example, the matrices (■(1&0@0&1)) and (■(1&0&0@0&1&0@0&0&1)) are unit matrices of order 2 and 3. An Identity Matrix is denoted by the letter I. [Note that a unit matrix is a particular case of a scalar matrix.]

Equal Matrices

Two matrices A and B are said to be equal matrices if A and B are of same order i.e. number of rows in A = number of rows in B and number of columns in A = number of columns in B, and their corresponding elements are equal i.e. the entries of A and B in the same position are equal. Otherwise, the matrices are said to be unequal.

If A and B are equal matrices, then we write A = B. Otherwise, we write A ≠ B.

For example:

The matrices A = (■(2&5@7&-4)) and B = (■(2&5@7&-4)) are equal, because both are of the same order 2 × 2 and their corresponding entries are equal. The matrices A = (■(2&3&0@7&-6&5)) and B = (■(2&4&0@7&-6&5)) are not equal, because (1, 2)th entry of A ≠ (1, 2)th entry of B, even though both matrices A and B are of the same order. The matrices (■(x@y)) and (■(2@-5)) are equal if and only if x = 2 and y = -5.

Worked Out Examples

Example 2: If a matrix has 6 elements, what are the possible orders it can have?

Solution:

If a matrix has 6 elements, then it can have any one of the following orders:

1 × 6, 6 × 1, 2 × 3 or 3 × 2.

Example 3: Construct a 2 × 2 matrix whose elements a_ij are given by a_ij = i + j.

Solution: Let, A = (■(a_11&a_12@a_21&a_22 )) Since aij = i + j, a11 = 1 + 1 = 2 a12 = 1 + 2 = 3 a21 = 2 + 1 = 3 a22 = 2 + 2 = 4 ∴ A = (■(2&3@3&4))

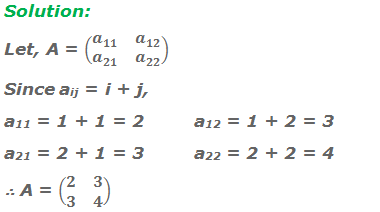
Example 4: Construct a 2 × 2 matrix A whose element a_ij are given by a_ij = 3i + 2j.

Solution: Let, A = (■(a_11&a_12@a_21&a_22 )) Since, aij = 3i + 2j, a11 = 3 . 1 + 2 . 1 = 5 a12 = 3 . 1 + 2 . 2 = 7 a21 = 3 . 2 + 2 . 1 = 8 a22 = 3 . 2 + 2 . 2 = 10 Hence, A = (■(5&7@8&10))

Example 5: Find the value of a, b, c and d if (■(a&-2@b&7)) = (■(2&c@3&2c+d)). Solution: Equating the corresponding elements we have, a = 2, b = 3, c = -2 and 2c + d = 7 or, 2 . (-2) + d = 7 or, -4 + d = 7 or, d = 7 + 4 or, d = 11 Hence, a = 2, b = 3, c = -2 and d = 11.

Do you have any questions regarding the matrix?

You can ask your questions or problems here, in the comment section below.

Matrix | What is Matrix?