Trigonometric Ratios of Compound Angles

0 comments

Trigonometric Ratios of Compound Angles

Trigonometric Ratios of Compound Angles


The sum or difference of two or more angles is said to be a compound angle. If A and B are two angles then A + B or A - B are known as the compound angles.



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver



********************


Install 10 Math Problems




********************


We express the trigonometrical ratios of compound angle A + B and A - B in terms of trigonometrical ratios of the angles A and B.


The trigonometrical ratios of the angles A + B and A - B are known as the addition and subtraction formula respectively.

 

Trigonometric Ratios of Compound Angle A + B (Addition Formula)


Let a revolving line start from OX and trace out an angle XOY = A and revolve further through an angle YOZ = B. Therefore, ∠XOZ = A + B.


Trigonometric Ratios of Compound Angle A + B (Addition Formula) Figure:

Let, P be any point on OZ. Draw PM perpendicular to OX and PN perpendicular to OY. From N draw NQ perpendicular to OX and NR perpendicular to PM.


Here, ∠RPN = 90° - ∠PNR     [∵  NR⊥MP]

               = ∠RNO   [∵  PN⊥OY]

               = ∠NOQ   [∵  RN ∥ OX]

               = A


Again, RMQN is a rectangle. So, MR = QN and RN = MQ.


Now from right angle ΔOMP,


sin(A + B) = "MP" /"OP" = "MR + RP" /"OP" = "QN + RP" /"OP" = "QN" /"OP" +"RP" /"OP" = "QN" /"ON" . "ON" /"OP" + "RP" /"NP" . "NP" /"OP" = sinA cosB + cosA sinB cos(A + B) = "OM" /"OP" = "OQ – MQ" /"OP" = "OQ – RN" /"OP" = "OQ" /"OP" – "RN" /"OP" = "OQ" /"ON" . "ON" /"OP" – "RN" /"NP" . "NP" /"OP" = cosA cosB – sinA sinB Hence, the sine formula and cos formula of compound angle (A + B) are: sin(A + B) = sinA cosB + cosA sinB cos(A + B) = cosA cosB - sinA sinB

Tangent Formula of Compound Angle (A + B)


tan(A + B) = "sin(A + B)" /"cos(A + B)" = "sinA cosB + cosA sinB" /("cosA cosB " -" sinA sinB" ) = ("sinA cosB + cosA sinB" /"cosA cosB" )/(("cosA cosB " -" sinA sinB" )/"cosA cosB" ) = ("sinA cosB" /"cosA cosB" + "cosA sinB" /"cosA cosB" )/("cosA cosB" /"cosA cosB" - "sinA sinB" /"cosA cosB" ) = "tanA + tanB" /"1 - tanA tanB" Hence, the tangent formula of compound angle (A + B) is, tan(A + B) = "tanA + tanB" /("1 " -" tanA tanB" )


Cotangent Formula of Compound Angle (A + B)


cot(A + B) = "cos(A + B)" /"sin(A + B)" = ("cosA cosB" - "sinA sinB" )/("sinA cosB" + "cosA sinB" ) = (("cosA cosB" - "sinA sinB" )/"sinA sinB" )/(("sinA cosB" + "cosA sinB" )/"sinA sinB" ) = ("cosA cosB" /"sinA sinB" - "sinA sinB" /"sinA sinB" )/("sinA cosB" /"sinA sinB" + "cosA sinB" /"sinA sinB" ) = ("cotA cotB" - "1" )/"cotB + cotA" Hence, the cotangent formula of compound angle (A + B) is, cot(A + B) = ("cotA cotB" - "1" )/"cotB + cotA"

Trigonometric Ratios of Compound Angle A – B (Subtraction Formula)


Let a revolving line start from OX and trace out an angle XOY = A and then revolve back through an angle YOZ = B. Therefore, ∠XOZ = A - B.


Trigonometric Ratios of Compound Angle A – B (Subtraction Formula) Figure:

Let, P be any point on the line OZ. Draw PM perpendicular to OX and PN perpendicular to OY. From N draw NQ perpendicular to OX and NR perpendicular to MP produced.


Here, ∠RPN = 90° - ∠PNR     [∵  PR⊥NR]

               = ∠RNY    [∵  PN⊥OY]

               = ∠XOY   [∵  OX ∥ NR]

               = A


Again, QMRN is a rectangle. So, QN = MR and QM = NR.


Now from right angle ΔOMP,


sin(A – B) = "MP" /"OP" = "MR – PR" /"OP" = "QN – RP" /"OP" = "QN" /"OP" – "PR" /"OP" = "QN" /"ON" . "ON" /"OP" – "PR" /"NP" . "NP" /"OP" = sinA cosB – cosA sinB cos(A – B) = "OM" /"OP" = "OQ + QM" /"OP" = "OQ + NR" /"OP" = "OQ" /"OP" + "NR" /"OP" = "OQ" /"ON" . "ON" /"OP" + "NR" /"NP" . "NP" /"OP" = cosA cosB + sinA sinB Hence, the sine formula and cos formula of compound angle (A - B) are: sin(A – B) = sinA cosB – cosA sinB cos(A – B) = cosA cosB + sinA sinB

Tangent Formula of Compound Angle (A – B)


tan(A – B) = ("sin(A " -" B)" )/("cos(A " -" B)" ) = ("sinA cosB " -" cosA sinB" )/"cosA cosB + sinA sinB" = (("sinA cosB " -" cosA sinB" )/"cosA cosB" )/("cosA cosB + sinA sinB" /"cosA cosB" ) = ("sinA cosB" /"cosA cosB" - "cosA sinB" /"cosA cosB" )/("cosA cosB" /"cosA cosB" + "sinA sinB" /"cosA cosB" ) = ("tanA " -" tanB" )/"1 + tanA tanB" Hence, the tangent formula of compound angle (A – B) is, tan(A – B) = ("tanA " -" tanB" )/"1 + tanA tanB"


Cotangent Formula of Compound Angle (A - B)


cot(A – B) = ("cos(A" - "B)" )/("sin(A" - "B)" ) = "cosA cosB + sinA sinB" /("sinA cosB" - "cosA sinB" ) = ("cosA cosB + sinA sinB" /"sinA sinB" )/(("sinA cosB" - "cosA sinB" )/"sinA sinB" ) = ("cosA cosB" /"sinA sinB" + "sinA sinB" /"sinA sinB" )/("sinA cosB" /"sinA sinB" - "cosA sinB" /"sinA sinB" ) = "cotA cotB + 1" /("cotB" - "cotA" ) Hence, the cotangent formula of compound angle (A - B) is, cot(A - B) = "cotA cotB + 1" /("cotB" - "cotA" )

List of Trigonometric Formula for Compound Angles A + B and A – B


1. sin(A + B) = sinA cosB + cosA sinB 2. cos(A + B) = cosA cosB – sinA sinB 3. tan(A + B) = "tanA + tanB" /("1 " -" tanA tanB" ) 4. cot(A + B) = ("cotA cotB" - "1" )/"cotB + cotA" 5. sin(A – B) = sinA cosB – cosA sinB 6. cos(A – B) = cosA cosB + sinA sinB 7. tan(A – B) = ("tanA " -" tanB" )/"1 + tanA tanB" 8. cot(A - B) = "cotA cotB + 1" /("cotB" - "cotA" )


Worked Out Examples


Example 1: Find the value of: (a) sin75° (b) tan15° Solution: sin75° = sin(45° + 30°) = sin45° cos30° + cos45° sin30° = "1" /√("2" ) . √("3" )/"2" + "1" /√("2" ) . "1" /"2" = √("3" )/("2" √("2" )) + "1" /("2" √("2" )) = (√("3" ) + "1" )/("2" √("2" )) tan15° = tan(45° - 30°) = ("tan45°" - "tan30°" )/"1 + tan45° tan30°" = ("1" - "1" /√("3" ))/("1" + "1" ."1" /√("3" ) ) = (√("3" ) - "1" )/(√("3" ) + "1" ) = (√("3" ) - "1" )/(√("3" ) + "1" ) × (√("3" ) - "1" )/(√("3" ) - "1" ) = (√("3" ) - "1" )^"2" /((√("3" ))^"2" - "1" ^"2" ) = ((√("3" ))^"2" – "2" .√("3" )."1" + "1" ^"2" )/("3 " - "1" ) = ("4" – "2" √("3" ) )/"2" = "2" – √("3" )


Example 2: If sinA = "3" /"5" and cosB = "5" /"13" , find the value of sin(A + B) Solution: Here, sinA = "3" /"5" and cosB = 5/13 ∴ cosA = √("1" – 〖"sin" 〗^"2" "A" ) = √("1" – "9" /"25" ) = √("16" /"25" ) = "4" /"5" ∴ sinB = √("1" – 〖"cos" 〗^"2" "B" ) = √("1" – "25" /"169" ) = √("144" /"169" ) = "12" /"13" Now, sin(A + B) = sinA cosB + cosA sinB = "3" /"5" . "5" /"13" + "4" /"5" . "12" /"13" = "15" /"65" + "48" /"65" = "63" /"65"
Example 3: If sinA = "1" /√("10" ) and sinB = "1" /√("5" ) , show that A + B = "Ï€" /"4" Solution: Here, sinA = "1" /√("10" ) and sinB = "1" /√("5" ) ∴ cosA = √("1" – 〖"sin" 〗^"2" "A" ) = √("1" – "1" /"10" ) = √("9" /"10" ) = "3" /√("10" ) ∴ cosB = = √("1" – 〖"sin" 〗^"2" "B" ) = √("1" – "1" /"5" ) = √("4" /"5" ) = "2" /√("5" ) Now, sin(A + B) = sinA cosB + cosA sinB = "1" /√("10" ) . "2" /√("5" ) + "3" /√("10" ) . "1" /√("5" ) = "2" /√("50" ) + "3" /√("50" ) = "5" /√("50" ) = "1" /√("2" ) = sin45° = sin "Ï€" /"4" ∴ A + B = "Ï€" /"4" . Proved.


Example 4: Prove that: ("cos14°" - "sin14°" )/"cos14° + sin14°" = "cot59°" Solution: RHS = cot59° = cot(45° + 14°) = ("cot45° cot14°" -" 1" )/"cot45° + cot14°" = ("cot14°" -" 1" )/"1 + cot14°" = ("cos14°" /"sin14°" " " -" 1" )/("1 + " "cos14°" /"sin14°" ) = (("cos14° " -" sin14°" )/"sin14°" )/("cos14° + sin14°" /"sin14°" ) = ("cos14° " -" sin14°" )/"cos14° + sin14°" = LHS. Proved.


Example 5: Prove that: sin35° + cos35° = √("2" ) cos10° Solution: Here, RHS = √("2" ) cos10° = √("2" ) cos(45° - 35°) = √("2" ) (cos45° cos35° + sin45° sin35°) = √("2" ) ("1" /√("2" ) ."cos35°" + "1" /√("2" ) ."sin35°" ) = cos35° + sin35° = LHS. Proved.


Example 6: Prove that: tan10° + tan35° + tan10° tan35° = 1 Solution: Here, 10° + 35° = 45° So, tan(10° + 35°) = tan45° or, "tan10° + tan35°" /("1 " –" tan10° tan35°" ) = 1 or, tan10° + tan35° = 1 – tan10° tan35° or, tan10° + tan35° + tan10° tan35° = 1 Hence proved.


Example 7: If A, B and C are the angles of a triangle then prove that: tanA + tanB + tanC = tanA tanB tanC. Solution: Here, A, B and C are angles of a triangle, So, A + B + C = 180° or, A + B = 180° - C or, tan(A + B) = tan(180° - C) or, "tanA + tanB" /("1 " –" tanA tanB" ) = - tanC or, tanA + tanB = - tanC + tanA tanB tanC or, tanA + tanB + tanC = tanA tanB tanC Hence proved.

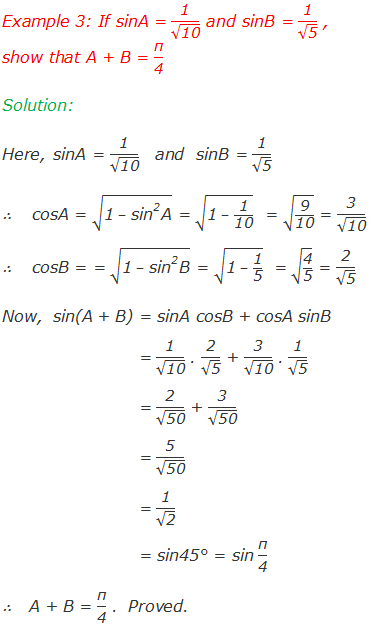
Do you have any questions regarding the trigonometric ratios of compound angles?

 

You can ask your questions or problems here, in the comment section below.

Labels:

About author: Min Rajbanshi

I am a school math teacher and a blogger since 2012. I do blogging on a variety of topics including math. Over the years, I've explored and written about a wide range of topics, with a particular emphasis on mathematics. My passion for education extends beyond the classroom, as I enjoy sharing knowledge and insights on various subjects through my blog.

0 comments:

Subscribe to: Post Comments (Atom)