Trigonometric Ratios of Multiple Angles

Trigonometric Ratios of Multiple Angles

If A is an angle, then 2A, 3A, 4A, 5A, etc are called multiple angles of A. In this section we will discuss about the trigonometric ratios of multiple angles 2A and 3A in terms of A.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

Install Quick Math Solver

********************

Install 10 Math Problems

********************

Trigonometric Ratios of Angle 2A in terms of A

Formula for sin2A

(a) sin2A = sin(A + A) = sinA cosA + cosA sinA = 2sinA cosA (b) sin2A = 2sinA cosA = "2sinA cosA" /"1" = "2sinA cosA" /(〖"cos" 〗^"2" "A + " 〖"sin" 〗^"2" "A" ) = ("2sinA cosA" /(〖"cos" 〗^"2" "A" ))/((〖"cos" 〗^"2" "A + " 〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" )) = ("2sinA " /"cosA" )/((〖"cos" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" ) " + " (〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" )) = "2tanA" /("1 + " 〖"tan" 〗^"2" "A" ) (c) sin2A = "2tanA" /("1 + " 〖"tan" 〗^"2" "A" ) = ("2" /"cotA" )/("1 + " "1" /(〖"cot" 〗^"2" "A" )) = "2" /"cotA" × (〖"cot" 〗^"2" "A" )/(〖"1 + cot" 〗^"2" "A" ) = "2cotA" /("1 + " 〖"cot" 〗^"2" "A" )

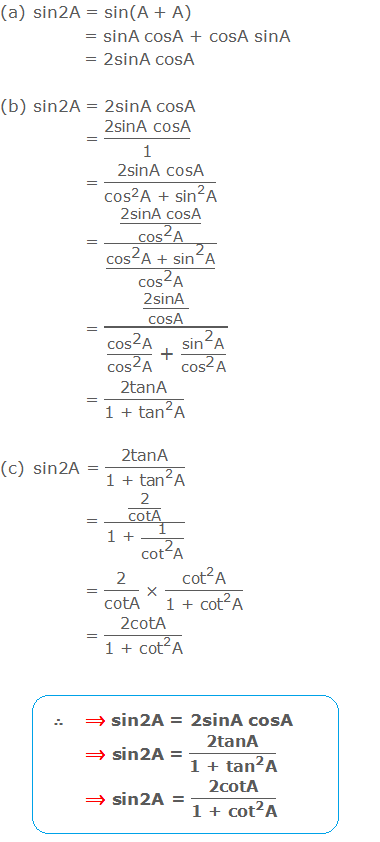
Formula for cos2A

(a) cos2A = cos(A + A) = cosA cosA – sinA sinA = cos2A – sin2A (b) cos2A = cos2A – sin2A = 1 - sin2A - sin2A = 1 - 2sin2A (c) cos2A = cos2A – sin2A = cos2A – (1 - cos2A) = 2cos2A – 1 (d) cos2A = cos2A – sin2A = "2sinA cosA" /"1" = (〖"cos" 〗^"2" "A – " 〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A + " 〖"sin" 〗^"2" "A" ) = ((〖"cos" 〗^"2" "A – " 〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" ))/((〖"cos" 〗^"2" "A + " 〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" )) = ((〖"cos" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" ) " – " (〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" ))/((〖"cos" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" ) " + " (〖"sin" 〗^"2" "A" )/(〖"cos" 〗^"2" "A" )) = ("1 – " 〖"tan" 〗^"2" "A" )/("1 + " 〖"tan" 〗^"2" "A" ) (e) cos2A = ("1 – " 〖"tan" 〗^"2" "A" )/("1 + " 〖"tan" 〗^"2" "A" ) = ("1 – " "1" /(〖"cot" 〗^"2" "A" ))/("1 + " "1" /(〖"cot" 〗^"2" "A" )) = (〖"cot" 〗^"2" "A – 1" )/(〖"cot" 〗^"2" "A" ) × (〖"cot" 〗^"2" "A" )/(〖"cot" 〗^"2" "A + 1" ) = (〖"cot" 〗^"2" "A – 1" )/(〖"cot" 〗^"2" "A + 1" )

The formula for tan2A and cot2A

(a) tan2A = tan(A + A) = "tanA + tanA" /"1 – tanA .tanA" = "2tanA" /("1 – " 〖"tan" 〗^"2" "A" ) (b) tan2A = "2tanA" /("1 – " 〖"tan" 〗^"2" "A" ) = ("2" /"cotA" )/(1 - 1/(〖"cot" 〗^"2" "A" )) = "2" /"cotA" × (〖"cot" 〗^"2" "A" )/(〖"cot" 〗^"2" "A – 1" ) = "2cotA" /(〖"cot" 〗^"2" "A – 1" ) (c) cot2A = cot(A + A) = "cotA .cotA – 1" /"cotA + cotA" = (〖"cot" 〗^"2" "A – 1" )/"2cotA " (d) cot2A = (〖"cot" 〗^"2" "A – 1" )/"2cotA " = ("1" /(〖"tan" 〗^"2" "A" ) " – 1" )/("2" /"tanA" " " ) = (〖"1 – tan" 〗^"2" "A" )/(〖"tan" 〗^"2" "A" ) × "tanA" /"2" = (〖"1 – tan" 〗^"2" "A" )/"2tanA"

Some Useful Results

(a) 1 + sin2A = cos2A + sin2A + 2sinAcosA = cos2A + 2cosA sinA + sin2A = (cosA + sinA)2 (b) 1 – sin2A = cos2A + sin2A – 2sinAcosA = cos2A – 2cosA sinA + sin2A = (cosA – sinA)2 (c) 1 + cos2A = 1 + cos2A – sin2A = 1 – sin2A + cos2A = cos2A + cos2A = 2cos2A (d) 1 – cos2A = 1 – (cos2A – sin2A) = 1 – cos2A + sin2A = sin2A + sin2A = 2sin2A

Trigonometric Ratios of Angle 3A in terms of A

(a) sin3A = sin(2A + A) = sin2A cosA + cos2A sinA = 2sinAcosAcosA + (1 – 2sin2A) sinA = 2sinA cos2A + sinA – 2sin3A = 2sinA(1 – sin2A) + sinA – 2sin3A = 2sinA – 2sin3A + sinA – 2sin3A = 3sinA – 4sin3A. (b) cos3A = cos(2A + A) = cos2A cosA – sin2A sinA = (2cos2A – 1)cosA – 2sinAcosAsinA = 2cos3A – cosA – 2sin2A cosA = 2cos3A – cosA – 2(1 – cos2A) cosA = 2cos3A – cosA – 2cosA + 2cos3A = 4cos3A – 3cosA. (c) tan3A = tan(2A + A) = "tan2A + tanA" /"1 – tan2A .tanA" = ("2tanA" /("1 – " 〖"tan" 〗^"2" "A" ) " + tanA" )/("1 – " "2tanA" /("1 – " 〖"tan" 〗^"2" "A" ) " .tanA" ) = ("2tanA + tanA – " 〖"tan" 〗^"3" "A" )/("1 – " 〖"tan" 〗^"2" "A – 2" 〖"tan" 〗^"2" "A" ) = ("3tanA – " 〖"tan" 〗^"3" "A" )/("1 – 3" 〖"tan" 〗^"2" "A" ).

List of the trigonometric formula for multiple angles 2A and 3A:

List of trigonometric formula for multiple angles 2A and 3A.

Geometrical Proof of 2A Formulae

Let O be the centre of the circle ABC and AB be a diameter (In the given figure below.). Let ∠CAB = A, then ∠COB = 2A [∵ Central angle is double of inscribed angle on same arc.]. ∠ACB = 90° [Inscribed angle on semi-circle.]

Figure of the circle for geometrical proof of 2A formula.

Let CM is perpendicular to AB. Then, ∠ACM = 90° – A, and hence ∠BCM = A.

Now from the right angle ΔOMC,

(a) sin2A = CM/(OC ) = 2CM/(2OC ) = 2CM/(AB ) = 2 . CM/(AC ). AC/(AB ) = 2sinA cosA. (b) cos2A = OM/(OC ) = 2OM/(2OC ) = 2OM/(AB ) = ((AO + OM) - (AO - OM))/(AB ) = ((AO + OM) - (BO - OM))/(AB ) = (AM - BM)/(AB ) = AM/(AB ) - BM/(AB ) = AM/(AC ) . AC/(AB ) - BM/(BC ) . BC/(AB ) = cosA cosB – sinA sinB = cos2A – sin2A. (c) tan2A = CM/(OM ) = 2CM/(2OM ) = 2CM/((AO + OM) - (AO - OM) ) = 2CM/((AO + OM) - (BO - OM) ) = 2CM/(AM - BM ) = (2CM/(AM ))/((AM - BM)/(AM ) ) = (2CM/(AM ))/(AM/(AM ) - BM/(AM )) = (2CM/(AM ))/(1 - BM/(CM ) .CM/(AM )) = 2tanA/(1 – tanA tanA) = 2tanA/(1 – tan^2 A).

Worked Out Examples:

Example 1: If sinA = 5/13 , find the value of sin2A, cos2A and tan2A. Solution: Here, sinA = 5/13. ∴ cosA = √(1 – 〖sin〗^2 A) = √(1-(5/13)^2 ) = √(1-25/169) = √(144/169) = 12/13 Now, sin2A = 2sinA cosA = 2 × 5/13 × 12/13 = 120/169 cos2A = cos2A – sin2A = (12/13)^2 – (5/13)^2 = 144/169 – 25/169 = (144 - 25)/169 = 119/169 tan2A = sin2A/cos2A = (120/169)/(119/169) = 120/119.

Example 2: If tanA = 3/4, find the value of sin2A, cos2A and tan2A. Solution: Here, tanA = 3/4 Now, sin2A = 2tanA/(1 + 〖tan〗^2 A) = (2 × 3/4)/(1 + 9/16) = (3/2)/(25/16) = 3/2 × 16/25 = 24/25 cos2A = (1 - 〖tan〗^2 A)/(1 + 〖tan〗^2 A) = (1 - 9/16)/(1 + 9/16) = (7/16)/(25/16) = 7/16 × 16/25 = 7/25 tan2A = 2tanA/(1 - 〖tan〗^2 A) = (2 × 3/4)/(1 - 9/16) = (3/2)/(7/16) = 3/2 × 16/7 = 24/7

Example 3: Express cos5A in terms of cosA. Solution: cos5A = cos(2A + 3A) = cos2A cos3A – sin2A sin3A = (2cos2A – 1)(4cos3A – 3cosA) – 2sinA cosA(3sinA – 4sin3A) = 8cos5A – 6cos3A – 4cos3A + 3cosA – 2cosA sin2A(3 – 4sin2A) = 8cos5A – 6cos3A – 4cos3A + 3cosA – 2cosA(1 – cos2A)(3 – 4 + 4cos2A) = 8cos5A – 6cos3A – 4cos3A + 3cosA – (2cosA – 2cos3A)(4cos2A - 1) = 8cos5A – 6cos3A – 4cos3A + 3cosA – 8cos3A + 2cosA + 8cos5A – 2cos3A = 16cos5A – 20cos3A + 5cosA

Example 4: Find the value of sin3A, cos3A and tan3A when sinA = √3/2 Solution: Here, sinA = √3/2 ∴ cosA = √(1- 〖sin〗^2 A) = √(1- 3/4) = √(1/4) = 1/2 ∴ tanA = sinA/cosA = (√3/2)/(1/2) = √3 Now, sin3A = 3sinA – 4sin3A = 3 × √3/2 - 4 × (3√3)/8 = (3√3)/2 - (3√3)/2 = 0 cos3A = 4cos3A – 3cosA = 4 × 1/8 - 3 × 1/2 = 1/2 - 3/2 = -1 tan3A = (3tanA - 〖tan〗^3 A)/(1 - 3〖tan〗^2 A) = (3√3 - 3√3)/(1 - 3×3) = 0/(1 - 9) = 0

Example 5: Prove that: (sinθ + sin2θ)/(1 + cosθ + cos2θ) = tanθ Solution: Here, LHS = (sinθ + sin2θ)/(1 + cosθ + cos2θ) = (sinθ + 2sinθ cosθ)/(cosθ + 1 + cos2θ) = (sinθ(1 + 2cosθ))/(cosθ + 2〖cos〗^2 θ) = (sinθ(1 + 2cosθ))/(cosθ(1 + 2cosθ)) = sinθ/cosθ = tanθ = RHS. Proved.

Example 6: Prove that: (1- cos2θ + sin2θ)/(1 + cos2θ + sin2θ) = tanθ Solution: Here, LHS = (1- cos2θ + sin2θ)/(1 + cos2θ + sin2θ) = (2〖sin〗^2 θ + 2sinθ cosθ)/(2〖cos〗^2 θ + 2sinθ cosθ) = (2sinθ(sinθ + cosθ))/(2cosθ(cosθ + sinθ)) = sinθ/cosθ = tanθ = RHS. Proved.

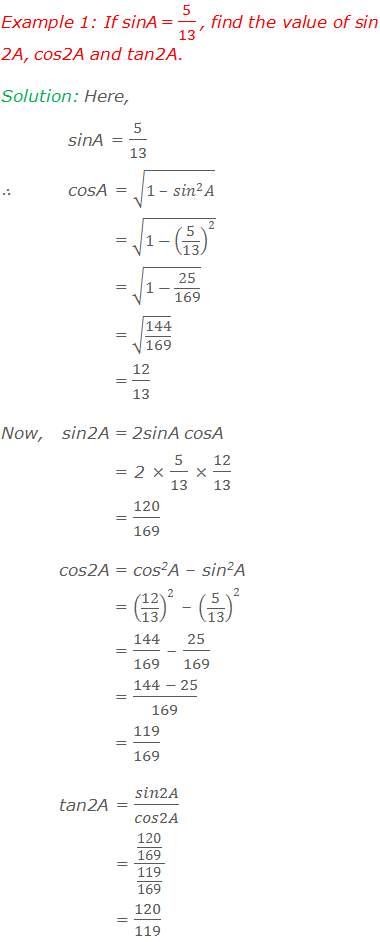
Example 7: Prove that: tan⁡(45°+ θ)= cos2θ/(1-sin2θ) Solution: Here, RHS = cos2θ/(1-sin2θ) = (〖cos〗^2 θ - 〖sin〗^2 θ)/(cosθ - sinθ)^2 = (cosθ + sinθ)(cosθ - sinθ)/(cosθ - sinθ)^2 = (cosθ + sinθ)/(cosθ - sinθ) = (cosθ/cosθ + sinθ/cosθ)/(cosθ/cosθ - sinθ/cosθ) = (1 + tanθ)/(1 - tanθ) = (tan45° + tanθ)/(tan45° - tanθ) = tan⁡(45°+ θ) = LHS. Proved.

Example 8: Show that: cos6θ – sin6θ = cos2θ(1 – ¼sin22θ) Solution: Here, LHS = cos6θ – sin6θ = (cos2θ)3 – (sin2θ)3 = (cos2θ – sin2θ)(cos4θ + cos2θ sin2θ + sin4θ) = cos2θ(cos4θ + 2cos2θ sin2θ + sin4θ – cos2θ sin2θ) = cos2θ[(cos2θ + sin2θ)2 – cos2θ sin2θ] = cos2θ[12 – ¼×4 cos2θ sin2θ] = cos2θ[1 - ¼ (2sinθ cosθ)2] = cos2θ[1 - ¼ (sin2θ)2] = cos2θ(1 - ¼ sin22θ) = RHS. Proved.

Example 9: Prove that: √3 cosec20° - sec20° = 4 Solution: Here, LHS = √3 cosec20° - sec20° = √3/(sin20°) - 1/(cos20°) = (√3 cos20° - sin20°)/(sin20° cos20°) = (2(√3 cos20° - sin20°))/(2sin20° cos20°) = 4(√3/2 cos20° - 1/2 sin20°)/(sin40°) = (4(sin60° cos20° - cos60°sin20°))/(sin40°) = (4sin(60°-20°))/(sin40°) = (4sin40°)/(sin40°) = 4 = RHS. Proved.

Example 10: Prove that: cot(45° + A) + tan(45° - A) = 2cos2A/(1 + sin2A) Solution: Here, LHS = cot(45° + A) + tan(45° - A) = (cot45° cotA - 1)/(cot45° + cotA) + (tan45°- tanA)/(tan45° tanA + 1) = (cotA - 1)/(1 + cotA) + (1 - tanA)/(tanA + 1) = (1/tanA - 1)/(1 + 1/tanA) + (1 - tanA)/(tanA + 1) = (1 - tanA)/(tanA + 1) + (1 - tanA)/(tanA + 1) = (2(1 - tanA))/(tanA + 1) = 2(1 - sinA/cosA)/(sinA/cosA + 1) = (2(cosA – sinA))/(cosA + sinA) = (2(cosA – sinA))/(cosA + sinA) × (cosA + sinA)/(cosA + sinA) = (2(〖cos〗^2 A - 〖sin〗^2 A))/(cosA + sinA)^2 = 2cos2A/(1 + sin2A) = RHS. Proved.

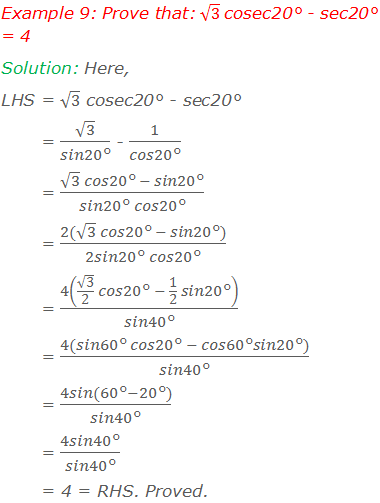
Do you have any questions regarding the trigonometric ratios of multiple angles?

You can ask your questions or problems here, in the comment section below.

0 comments:

Subscribe to: Post Comments (Atom)