Trigonometric Ratios of Standard Angles

Trigonometric Ratios of Standard Angles

 

In trigonometry, 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180° etc. are considered as the standard angles. We can derive the values of trigonometric ratios of standard angles geometrically.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

We should remember those values for the calculations in trigonometry. Here is the geometrical procedure for the derivation of trigonometric ratios of standard angles.

 

 

Trigonometric ratios of 45°

 

Let OX be the initial line and trace out an ∠XOP = 45°. From Q, a point on OP, draw QN⊥OX. Then ∠NQO = 90° – 45° = 45°. Therefore it is an isosceles triangle, i.e. ON = NQ. Let ON = NQ = a.

From the right angled triangle ONQ, using Pythagoras relation, 

OQ² = ON² + NQ²

                  = a² + a²

                  = 2a²

∴        OQ  = a√2

 

Now for right angled triangle ONQ with angle of reference ∠NOQ = 45°,

Trigonometric ratios of 60° and 30°

 

Let ABC be a triangle in which AB = BC = CA and hence ∠A = ∠B = ∠C = 60°. From A draw AD⊥BC. Then ∠BAD = ∠CAD = 30° and BD = CD. Let AB = BC = CA = 2a. So, BD = CD = a.

Now, from right angled DABD, 

          AD² = AB² – BD²

                  = 4a² – a²

                  = 3a²

∴         AD = a√3

 

Now, in right angled DABD with angle of reference ∠ABD = 60°,

And, with the angle of reference ∠BAD = 30°,

Trigonometric ratios of 0°

 

Let OX be the initial line and trace out an ∠XOP = θ. Let Q be a point on OP. Draw QM⊥OX.

When θ is decreased and tends to be 0° keeping OM constant, then QM = 0 and OQ = OM.

 

Now, from right angled triangle MOQ with angle of reference θ = 0°,

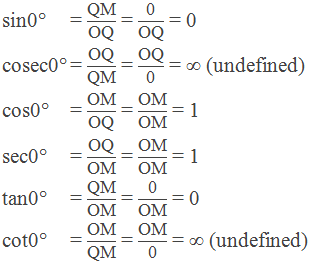
Trigonometric ratios of 90°

 

Let OX be the initial line and trace out an ∠XOP = θ. Let Q be a point on OP. Draw QM⊥OX.

When θ is increased and tends to be 90° keeping MQ constant, then OM = 0 and OQ = MQ.

 

Now, from right angled triangle MOQ with angle of reference θ = 90°,

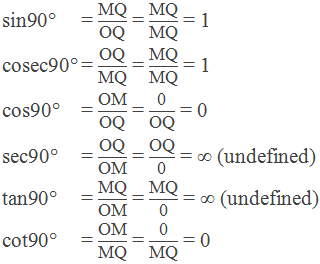
Table of Trigonometric Ratios of Standard Angles

Worked Out Examples

 

Example 1: Find the value of sin²30° + sin²45° + sin²60°

 

Solution: Here,

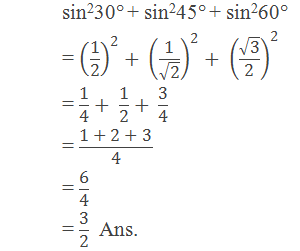
Example 2: Find the value of:

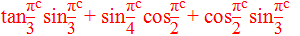
Solution: Here,

Example 3: Prove that:

Solution: Here,

Example 4: Find the value of x: sin60°cos30° + x sin45°cos45° = sin30°cos60°

 

Solution: Here,

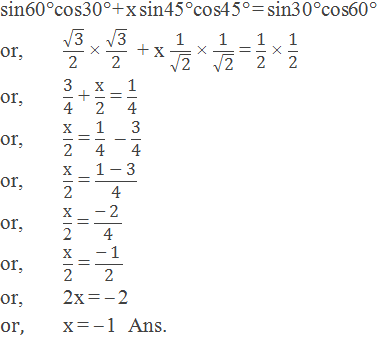
Example 5: In the given figure, the distance between house B and House C is 20m and ∠BCA = 30°. Calculate the distance between house A and B.

 

Solution: Here,

ΔABC is a right angled triangle. BC = 20m, ∠BCA = 30° and ∠BAC = 90°

          Sin30° = AB/BC

or,     ½ = AB/20m

or,     2AB = 20m

or,     AB = 20m/2

or,     AB = 10m

 

Hence, the distance between house A and B is 10m. 

If you have any question or problems regarding the Trigonometric Ratios of Standard Angles, you can ask here, in the comment section below.

 

Was this article helpful? LIKE and SHARE with your friends…