Trigonometric Ratios

Trigonometric Ratios

Trigonometry deals with the measurement of triangles, that is, it deals with the relationship between the sides and angles of triangles.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

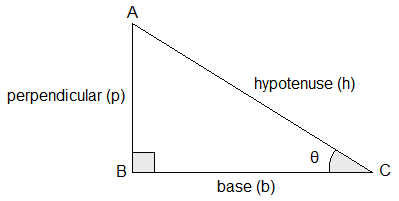
Let us consider a right-angled triangle ABC in which ∠ABC = 90°. This triangle consists of a right angle, two acute angles and three sides. These are called elements of a right-angled triangle.

One of the acute angle is considered as the angle of reference. This angle of reference is used for naming the sides of a right-angled triangle. 

The side opposite to the angle of reference is called perpendicular and it is denoted by the letter p. The side opposite to the right angle is called hypotenuse and it is denoted by the letter h. The remaining side is base and it is denoted by b. Clearly, the base is the side between right angle and the angle of reference.

If ∠ACB = θ is taken as the angle of reference, then AB, AC and BC are perpendicular, hypotenuse and base of the right angled triangle ABC. 

If ∠BAC = φ is the angle of reference, then BC, AC and AB respectively are perpendicular, hypotenuse and base of the same right angled triangle ABC. 

So, the name of the sides of a right angled triangle depends on the choice of the angle of reference.

With the help of three sides of a right angled triangle, six ratios can be derived taking any one acute angle as the angle of reference.

Six ratios are:

(i)          AB/BC

(ii)         AB/CA

(iii)        BC/AB

(iv)       BC/CA

(v)        CA/AB

(vi)       CA/BC

These ratios are commonly known as trigonometric ratios.

If ∠ACB = θ is taken as angle of reference, then

AB = perpendicular (p)

CA = hypotenuse (h)

BC = base (b)

Now, the six trigonometric ratios of DABC right angled at B with angle of reference θ are as follows:

(i)          AB/CA = p/h = Sine of angle θ = Sinθ

(ii)         CA/AB = h/p = Cosecant of angle θ = Cosecθ

(iii)        BC/CA = b/h = Cosine of angle θ = Cosθ

(iv)       CA/BC = h/b = Secant of angle θ = Secθ

(v)        AB/BC = p/b = Tangent of angle θ = Tanθ

(vi)       BC/AB = b/p = Cotangent of angle θ = Cotθ

Traditionally, trigonometric ratios are defined on the angles of a triangle as above. But, now-a-days these trigonometric ratios are defined on the angles of any magnitude as below.

Let us consider an angle θ placed in the standard position. Draw circle with centre at O and radius r. Let the circle intersect the terminal line at some point P(x, y) as shown in the figure. Draw perpendicular PM from P to x-axis. Then, OM = x, PM = y and OP = r. For any angle θ, the six trigonometric ratios can be defined in terms of x-coordinate ‘x’, y-coordinate ‘y’ and the radius ‘r’ by the formula.

Sinθ = y/r          Cosθ = x/r         Tanθ = y/x

Cosecθ = r/y      Secθ = r/x         Cotθ = x/y

Fundamental Relations of Trigonometric Ratios

There are generally 3 fundamental relations of trigonometric ratios.

(a) Reciprocal Relations

(b) Quotient Relations

(c)  Pythagorean Relations

Let us consider a circle centered at the origin O and having radius r. Let P(x, y) be any point on the circle. Join OP and let ∠XOP = θ. Draw perpendicular PM from P to x-axis. Then OM = x, PM = y and OP = r.

Now, Sinθ = y/r          Cosθ = x/r         Tanθ = y/x

        Cosecθ = r/y      Secθ = r/x         Cotθ = x/y

(a) Reciprocal Relations: Out of six ratios, there are 3 pairs which form reciprocal relations. These 3 pairs are: sinθ and cosecθ, cosθ and secθ and tanθ and cotθ.

(1) We know, y/r × r/y = 1

or,    sinθ × cosecθ = 1 ……….. (i)

or,    sinθ = 1/cosecθ …………. (ii)

or,    cosecθ = 1/sinθ …………. (iii)

(2) x/r × r/x = 1

or,    cosθ × secθ = 1 ………….. (iv)

or,    cosθ = 1/secθ …………….. (v)

or,    secθ = 1/cosθ …………….. (vi)

(3) y/x × x/y = 1

or,    tanθ × cotθ = 1 …………… (vii)

or,    tanθ = 1/cotθ …………..… (viii)

or,    cotθ = 1/tanθ …………….. (ix)

Hence, the reciprocal relations are:

sinθ . cosecθ = 1	sinθ = 1/cosecθ	cosecθ = 1/sinθ
cosθ . secθ = 1	cosθ = 1/secθ	secθ = 1/cosθ
tanθ . cotθ = 1	tanθ = 1/cotθ	cotθ = 1/tanθ

 

(b) Quotient Relations

(1)We have,

tanθ = y/x = (y/r)/(x/r) = sinθ/cosθ = secθ/cosecθ

(2)Again,

cotθ = x/y = (x/r)/(y/r) = cosθ/sinθ = cosecθ/secθ

Hence, the quotient relations are:

tanθ = sinθ/cosθ	cotθ = cosθ/sinθ
tanθ = secθ/cosecθ	cotθ = cosecθ/secθ

 

(c) Pythagorean Relations

(1) By Pythagoras theorem,

x² + y² = r²

Dividing both sides by r², we get

(x/r)2 + (y/r)² = 1

or,    (cosθ)² + (sinθ)² = 1

or,    sin²θ + cos²θ = 1 ………………. (i)

or,    sin²θ = 1 – cos²θ ………………. (ii)

or,    cos²θ = 1 – sin²θ ………………. (iii)

(2) r² – y² = x²

Dividing both sides by x², we get

(r/x)² – (y/x)² = 1

or,    (secθ)² – (tanθ)² = 1

or,    sec²θ – tan²θ = 1 ………………. (iv)

or,    sec²θ = 1 + tan²θ ………………. (v)

or,    tan²θ = sec²θ – 1 …………….... (vi)

(3) r² – x² = y²

Dividing both sides by y², we get

(r/y)² – (x/y)² = 1

or,    (cosecθ)² – (cotθ)² = 1

or,    cosec²θ – cot²θ = 1 ……………. (vii)

or,    cosec²θ = 1 + cot²θ …………… (viii)

or,    cot²θ = cosec²θ – 1 ……….….. (ix)

Hence, the Pythagorean relations are:

sin2θ + cos2θ = 1	sec2θ – tan2θ = 1	cosec2θ – cot2θ = 1
sin2θ = 1 – cos2θ	sec2θ = 1 + tan2θ	cosec2θ = 1 + cot2θ
cos2θ = 1 – sin2θ	tan2θ = sec2θ – 1	cot2θ = cosec2θ – 1

Derived Relations:

From the above relations, it is clear that the following relations are also true.

(1) sinθ . cosecθ = 1. So, sin²θ . cosec²θ = 1, sin³θ . cosec³θ = 1 and so on.

(2) sinθ = 1/cosecθ. So, sin²θ = 1/cosec²θ, sin³θ = 1/cosec³θ and so on.

(3) cosecθ = 1/sinθ. So, cosec²θ = 1/sin²θ, cosec³θ = 1/sin³θ and so on.

(4) cosθ . secθ = 1. So, cos²θ . sec²θ = 1, cos³θ . sec³θ = 1 and so on.

(5) cosθ = 1/secθ. So, cos²θ = 1/sec²θ, cos³θ = 1/sec³θ and so on.

(6) secθ = 1/cosθ. So, sec²θ = 1/cos²θ, sec³θ = 1/cos³θ and so on.

(7) tanθ . cotθ = 1. So, tan²θ . cot²θ = 1, tan³θ . cot³θ = 1 and so on.

(8) tanθ = 1/cotθ. So, tan²θ = 1/cot²θ, tan³θ = 1/cot³θ and so on.

(9) cotθ = 1/tanθ. So, cot²θ = 1/tan²θ, cot³θ = 1/tan³θ and so on.

(10) tanθ = sinθ/cosθ. So, tan²θ = sin²θ/cos²θ, tan³θ = sin³θ/cos³θ and so on.

(11) tanθ = secθ/cosecθ. So, tan²θ = sec²θ/cosec²θ, tan³θ = sec³θ/cosec³θ and so on.

(12) cotθ = cosθ/sinθ. So, cot²θ = cos²θ/sin²θ, cot³θ = cos³θ/sin³θ and so on.

(13) cotθ = cosecθ/secθ. So, cot²θ = cosec²θ/sec²θ, cot³θ = cosec³θ/sec³θ and so on.

(14) sin²θ = 1 – cos²θ. So, sinθ = √(1 – cos²θ)

(15) cos²θ = 1 – sin²θ. So, cosθ = √(1 – sin²θ)

(16) sec²θ = 1 + tan²θ. So, secθ = √(1 + tan²θ)

(17) tan²θ = sec²θ – 1. So, tanθ = √( sec²θ – 1)

(18) cosec²θ = 1 + cot²θ. So, cosecθ = √(1 + cot²θ)

(19) cot²θ = cosec²θ – 1. So, cotθ = √( cosec²θ – 1)

Follow: Trigonometric Identities for worked out examples.