
Multiplication of Matrices
Let A and B be two matrices. Then, the multiplication of matrices A and B i.e.
product of A and B is denoted by AB if it is defined. The product AB can be
defined or cannot be defined. It depends on the order of A and B.
********************
10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.
********************
********************
Two matrices A and B are said to be conformable or compatible for the product AB if and only if the number of columns in A is equal to the number of rows in B. It means we can define the product AB only when the number of columns in A and number of rows in B are same. If this condition is not satisfied then the product of matrices A and B cannot be performed. In such a situation, matrices A and B are not conformable for multiplication.
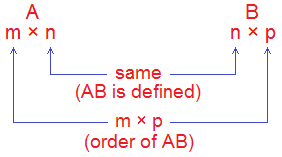
If A and B are conformable for the
product AB, then the number of rows in A followed by the number of columns in B
gives the order of the product AB.
Let the order of A be m × n and that of B
be n × p. Here, number of columns of A and the number of rows of B are the same.
So, the matrices A and B are conformable for the product AB. Number of rows in
A is m and number of columns in B is p. So, the order of product AB is m × p.
If two matrices A and B are conformable
or compatible for the product AB, it is not necessary that they are also
conformable or compatible for the product BA. If A and B are square matrices of
the same order, then they are conformable for the product AB as well as BA.
The element in row i and column j of the
product AB is obtained by multiplying the elements in the ith row of
A by the corresponding elements in jth column of B, and then by
adding up the resulting products.
∴ (i, j)th
element of the product AB = Sum of the products of the elements of ith
row of A with the corresponding elements of jth column of B.
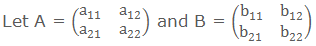
Here, order of the product AB will be 2 × 2. If cij
denotes the elements of the product matrix AB, then

Working Rule (Steps for multiplying matrices):
First of all guess the order of product AB and
write down as follows:

Examples:

Properties of Matrix Multiplication
1. Multiplication of matrices, generally, is not commutative, i.e. AB ≠ BA, in general.
i.
When the matrix AB is
defined, it not always necessary that BA can also be defined. For example, if
the matrix A is m × n and the matrix B is n × p, AB exists whereas BA does not
exist because p ≠ m.
ii.
When both AB and BA are
defined, it is not necessary that they should be of the same type. For example,
if the matrix A is of order m × n and the matrix B is of order n × m, both the
matrices AB and BA exist but AB is of order m × m while BA is of order n × n.
iii. When A and B are the square matrices of same order, then both AB and BA exist, but they are not necessarily equal. For example,

iv.
But, sometimes AB and BA
are also equal. For example,

Hence in general AB ≠ BA.
2. Multiplication of matrices is associative i.e. if matrices A, B and C are conformable for multiplication, then (AB)C = A(BC).
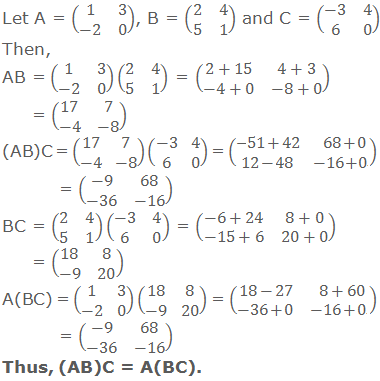
3. Multiplication of matrices
is distributive with respect to addition, i.e if matrices A, B and C are compatible
for the requisite addition and multiplication, then A(B + C) = AB + AC and (A +
B)C = AC + BC.
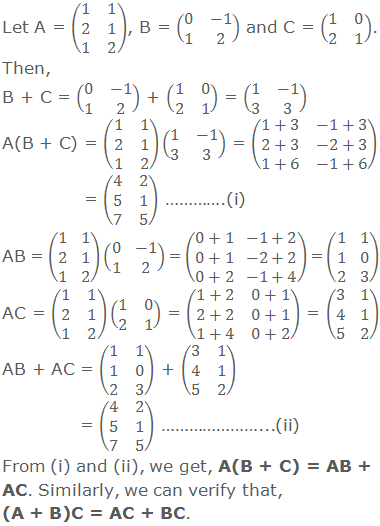
4. If A is a square matrix and
I is an identity matrix of same order, then AI = IA = A.

Note: Multiplication of matrices
gives us some results which are different from the results obtained in the case
of numbers. Some of these results illustrated in the following examples:
i.
If AB is a null matrix, it
does not imply that at least one of the matrices A or B must be a zero matrix.
For example,
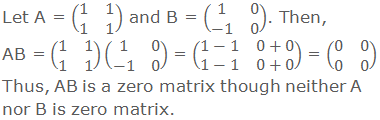
ii.
Cancellation law may not
hold in matrix multiplication. For example,

Worked Out Examples





Do you have any questions regarding the multiplication of matrices?
You can ask your questions or problems here, in the comment section below.



0 comments: