Operation of Matrices

0 comments

Operation of Matrices

Operation of Matrices


Here in Operation of Matrices, we deal with the Addition of Matrices, Subtraction of Matrices and Multiplication of a Matrix by a scalar (real number).



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems


********************


Addition of Matrices


If A and B are two matrices of the same order, then A and B are said to be Conformable or Compatible for addition. The sum of A and B is denoted by A + B and it is obtained by adding corresponding elements of matrices A and B.


The matrix A + B will be of the same order as each of the matrices A and B is.


If A = (■(a_11&a_12&a_13@a_21&a_22&a_23 )) and B = (■(b_11&b_12&b_13@b_21&b_22&b_23 )) Then, A + B = (■(a_11+b_11&a_12+b_12&a_13+b_13@a_21+b_21&a_22+b_22&a_23+b_23 )) For example: If A = (■(1&2&3@4&-3&7)) and B = (■(-3&4&7@8&9&-3)) Then, A + B = (■(1&2&3@4&-3&7)) + (■(-3&4&7@8&9&-3)) = (■(1-3&2+4&3+7@4+8&-3+9&7-3)) = (■(-2&6&10@12&6&4))


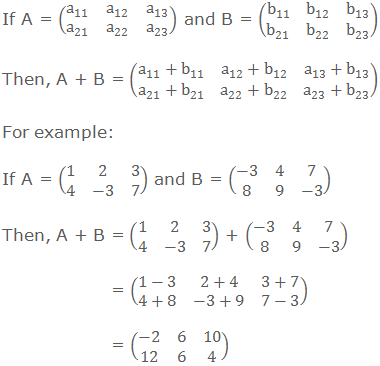
Subtraction of Matrices


If A and B are two matrices of the same order, then they are said to be conformable for subtraction. The difference of the matrix B from A is denoted by A – B and it is obtained by subtracting the elements of B from the corresponding elements of A.


The order of the matrix A – B is same as the order of A or B.


If A = (■(a_11&a_12&a_13@a_21&a_22&a_23 )) and B = (■(b_11&b_12&b_13@b_21&b_22&b_23 )) Then, A – B = (■(a_11-b_11&a_12-b_12&a_13-b_13@a_21-b_21&a_22-b_22&a_23-b_23 )) For example: If A = (■(1&2&3@4&-3&7)) and B = (■(-3&4&7@8&9&-3)) Then, A – B = (■(1&2&3@4&-3&7)) – (■(-3&4&7@8&9&-3)) = (■(1+3&2-4&3-7@4-8&-3-9&7+3)) = (■(4&-2&-4@-4&-12&10)) B – A = (■(-3&4&7@8&9&-3)) – (■(1&2&3@4&-3&7)) = (■(-3-1&4-2&7-3@8-4&9+3&-3-7)) = (■(-4&2&4@4&12&-10))

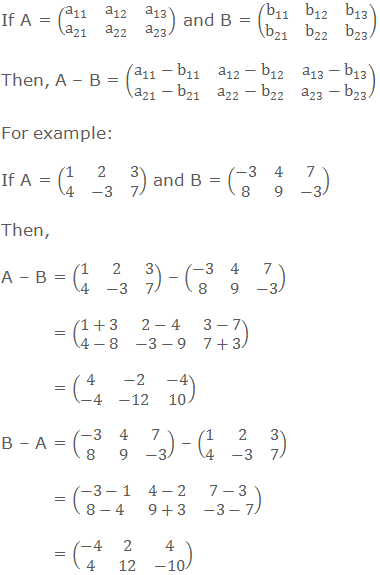
Multiplication of a Matrix by a scalar (real number)


If A is any matrix and k is any constant or a scalar, then the matrix obtained by multiplying each element of A by k is denoted by kA and it is called scalar multiple of A by k.


The order of the matrix kA is the same as the order of the matrix A.


If A = (■(a_11&a_12&a_13@a_21&a_22&a_23 )), then kA = (■(ka_11&ka_12&ka_13@ka_21&ka_22&ka_23 )) For example, If A = (■(2&4&6@-8&-10&-12)), then 2A = (■(4&8&12@-16&-20&-24)) –1A = (■(-2&-4&-6@8&10&12)) 1/2 A = (■(1&2&3@-4&-5&-6)) 0A = (■(0&0&0@0&0&0))


Algebraic Properties of Matrix Addition

The addition of matrices satisfies the following properties:

1.   Closure property:

If A and B are two matrices of the same order, then their sum A + B is also a matrix of the same order as that of A or B.

Let A = (■(2&4@3&5)) and B = (■(6&5@2&1)), the order of A and B is 2 × 2. Now, A + B = (■(2&4@3&5)) + (■(6&5@2&1)) = (■(8&9@5&6)) which is again 2 × 2 matrix. Hence the closure property is satisfied.

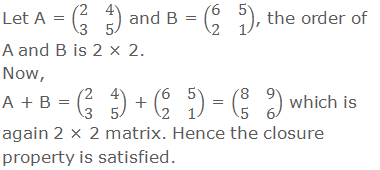
2.   Commutative property:

If A and B are two matrices of the same order, then A + B = B + A.

Let A = (■(2&4@6&8)) and B = (■(7&-2@8&4)) Then, A + B = (■(2&4@6&8)) + (■(7&-2@8&4)) = (■(9&2@14&12)) B + A = (■(7&-2@8&4)) + (■(2&4@6&8)) = (■(9&2@14&12)) ∴ A + B = B + A Hence the commutative property is satisfied.

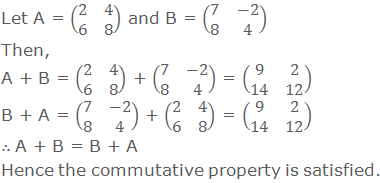
3.   Associative properties:

If A, B and C are three matrices of the same order, then (A + B) + C = A + (B + C)

Let A = (■(1&2@3&4)), B = (■(5&6@7&8)) and C = (■(9&10@11&12)) Then, (A + B) + C = [(■(1&2@3&4)) + (■(5&6@7&8)) ] + (■(9&10@11&12)) = (■(6&8@10&12)) + (■(9&10@11&12)) = (■(15&18@21&24)) A + (B + C) = (■(1&2@3&4)) + [(■(5&6@7&8))+ (■(9&10@11&12)) ] = (■(1&2@3&4)) + (■(14&16@18&20)) = (■(15&18@21&24)) ∴ (A + B) + C = A + (B + C) Hence the associative property is satisfied.

4.   Existence of additive identity:

If A is any matrix, then there exists a null matrix O of the same order such as A + O = O + A = A.

Let A = (■(1&2@3&4)) and O = (■(0&0@0&0)). Then, A + O = (■(1&2@3&4)) + (■(0&0@0&0)) = (■(1&2@3&4)) = A O + A = (■(0&0@0&0)) + (■(1&2@3&4)) = (■(1&2@3&4)) = A ∴ A + O = O + A = A The null matrix O = (■(0&0@0&0)) is the additive identity of any 2 × 2 matrix A.

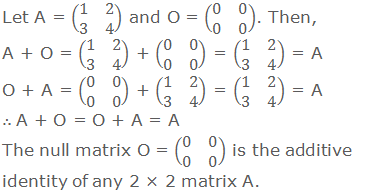
5.   Existence of additive inverse:

If A is a matrix of any order, then there exists another matrix –A or same order such that A + (-A) = (-A) + A = O, the additive identity.

Let A = (■(2&-3@4&-5)). Then, -A = (■(-2&3@-4&5)) Now, A + (-A) = (■(2&-3@4&-5)) + (■(2&-3@4&-5)) = (■(0&0@0&0)) = O (-A) + A = (■(2&-3@4&-5)) + (■(2&-3@4&-5)) = (■(0&0@0&0)) = O ∴ A + (-A) = (-A) + A = O ∴ -A is called the additive inverse of A and vice-versa.

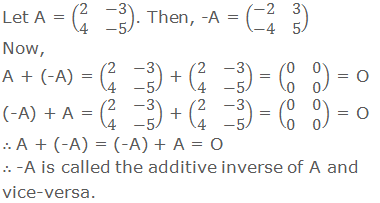
6.   If A and B are the matrices of the same order and k is a scalar, then k(A + B) = kA + kB.

Let A = (■(3&-7@8&4)), B = (■(-4&6@-2&8)) and k = 2 Then, k(A + B) = 2[(■(3&-7@8&4)) + (■(-4&6@-2&8)) ] = 2(■(-1&-1@6&12)) = (■(-2&-2@12&24)) kA + kB = 2(■(3&-7@8&4)) + 2(■(-4&6@-2&8)) = (■(6&-14@16&8)) + (■(-8&12@-4&16)) = (■(-2&-2@12&24)) ∴ k(A + B) = kA + kB.

7.   If A is a matrix and c, k are any two scalars, then (c + k)A = cA + kA.

Let c = 2 and k = 3 and A = (■(8&2@4&6)). Then, (c + k)A = (2 + 3)(■(8&2@4&6)) = 5(■(8&2@4&6)) = (■(40&10@20&30)) cA + kA = 2(■(8&2@4&6)) + 3(■(8&2@4&6)) = (■(16&4@8&12)) + (■(24&6@12&18)) = (■(40&10@20&30)) ∴ (c + k)A = cA + kA.

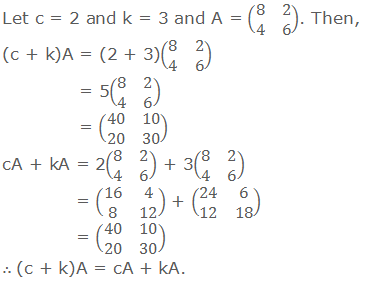
8.   If c, k are any two scalars and A is a matrix, then c(kA) = (ck)A.

Let c = -2 and k = 4 and A = (■(4&5@-3&7)). Then, c(kA) = -2[4(■(4&5@-3&7)) ] = -2(■(16&20@-12&28)) = (■(-32&-40@24&-56)) (ck)A = (-2×4)(■(4&5@-3&7)) = -8(■(4&5@-3&7)) = (■(-32&-40@24&-56)) ∴ c(kA) = (ck)A.

Worked Out Examples


Example 1: If A = (■(1&3&-4@7&-3&0)) and B = (■(-5&3&0@2&4&-4)), find A + B. Solution: Here, A = (■(1&3&-4@7&-3&0)) and B = (■(-5&3&0@2&4&-4)) Now, A + B = (■(1&3&-4@7&-3&0)) + (■(-5&3&0@2&4&-4)) = (■(1-5&3+3&-4+0@7+2&-3+4&0-4)) = (■(-4&6&-4@9&1&-4))


Example 2: If P = (■(2&-3@1&4@6&7)) and Q = (■(-2&7@0&-5@3&8)), find P – Q and Q – P. Solution: Here, P = (■(2&-3@1&4@6&7)) and Q = (■(-2&7@0&-5@3&8)) Now, P – Q = (■(2&-3@1&4@6&7)) - (■(-2&7@0&-5@3&8)) = (■(2+2&-3-7@1-0&4+5@6-3&7-8)) = (■(4&-10@1&9@3&-1)) Q – P = (■(-2&7@0&-5@3&8)) - (■(2&-3@1&4@6&7)) = (■(-2-2&7+3@0-1&-5-4@3-6&8-7)) = (■(-4&10@-1&-9@-3&1))
Example 3: If A = (■(2&-1&3@1&4&-2)), find 2A. Solution: Here, A = (■(2&-1&3@1&4&-2)) ∴ 2A = 2(■(2&-1&3@1&4&-2)) = (■(2×2&2×(-1)&2×3@2×1&2×4&2×(-2))) = (■(4&-2&6@2&8&-4))


Example 4: Given that A = (■(2&0@1&2)) and B = (■(2&0@-1&2)), find A + 2B. Solution: Here, A = (■(2&0@1&2)) and B = (■(2&0@-1&2)) A + 2B = (■(2&0@1&2)) + 2(■(2&0@-1&2)) = (■(2&0@1&2)) + (■(4&0@-2&4)) = (■(2+4&0+0@1-2&2+4)) = (■(6&0@-1&6))


Example 5: if A = (■(2&0@-3&1)) and B = (■(0&1@-2&3)), find 2A – 3B. Solution: Here, A = (■(2&0@-3&1)) and B = (■(0&1@-2&3)) 2A – 3B = 2(■(2&0@-3&1)) - 3(■(0&1@-2&3)) = (■(4&0@-6&2)) - (■(0&3@-6&9)) = (■(4-0&0-3@-6+6&2-9)) = (■(4&-3@0&-7))


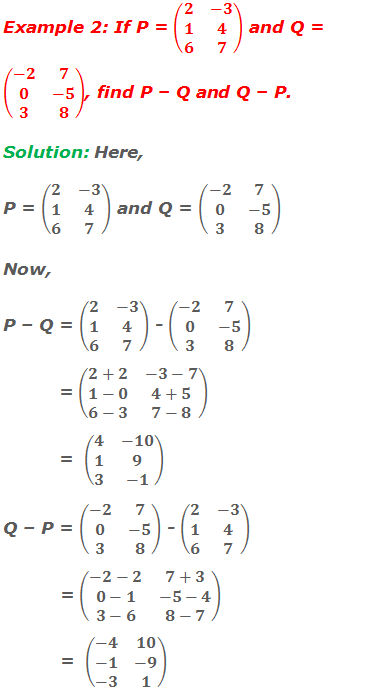
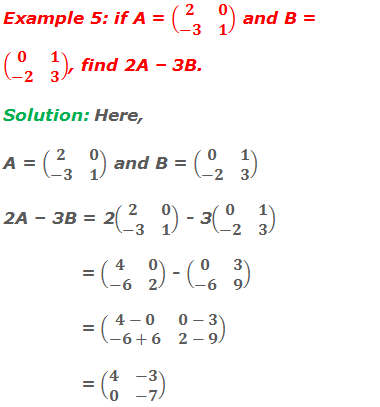
Do you have any questions regarding the enlargement and reduction?

You can ask your questions or problems here, in the comment section below.

Labels:

0 comments:

Subscribe to: Post Comments (Atom)