Vector Geometry

Vector Geometry

Vector Geometry: We can study different properties and relations relating to geometry with the help of vectors. Such a study is known as the Vector Geometry.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

Install Quick Math Solver

********************

Install 10 Math Problems

********************

Here are 12 geometrical theorems and their proofs by vector method.

Theorem 1: Midpoint Formula

If ( "a" ) ⃗ and ( "b" ) ⃗ are position vectors of two points A and B respectively and M is the middle point of the line segment AB, then the position vector of M is "1" /"2" (( "a" ) ⃗+( "b" ) ⃗ ). Proof: Let AB be a line segment and O be the origin. Position vectors of points A and B, ("OA" ) ⃗ = ( "a" ) ⃗ and ("OB" ) ⃗ = ( "b" ) ⃗. Suppose, M be the middle point of the line segment AB. ∴ ("AM" ) ⃗ = ("MB" ) ⃗ = "1" /"2" ("AB" ) ⃗ Now, ("OM" ) ⃗ = ("OA" ) ⃗ + ("AM" ) ⃗ = ("OA" ) ⃗ + "1" /"2" ("AB" ) ⃗ = ("OA" ) ⃗ + "1" /"2" (("AO" ) ⃗+("OB" ) ⃗ ) = ("OA" ) ⃗ + "1" /"2" (–("OA" ) ⃗+("OB" ) ⃗ ) = (" a " ) ⃗ + "1" /"2" (–(" a " ) ⃗+(" b " ) ⃗ ) = ("2" ( "a" ) ⃗ - ( "a" ) ⃗ + ( "b" ) ⃗)/"2" = (( "a" ) ⃗ + ( "b" ) ⃗)/"2" = "1" /"2" (( "a" ) ⃗+( "b" ) ⃗ ) Hence, position vector of M = ("OM" ) ⃗ = "1" /"2" (( "a" ) ⃗+( "b" ) ⃗ ). Proved.

Theorem 2: Section Formula for Internal Division

If ( "a" ) ⃗ and ( "b" ) ⃗ be the position vectors of two points A and B respectively and the point M divides the line segment AB internally in the ratio m : n, then the position vector of M is ("m" ( "b" ) ⃗" + n" ( "a" ) ⃗)/"m + n" . Proof: Let AB be a line segment and O be the origin. Position vectors of A and B are ("OA" ) ⃗ = ( "a" ) ⃗ and ("OB" ) ⃗ = ( "b" ) ⃗. Suppose, M divides the line segment AB internally in the ratio of m : n. ∴ ("AM" ) ⃗/("MB" ) ⃗ = "m" /"n" or, n("AM" ) ⃗ = m("MB" ) ⃗ or, n(("AO" ) ⃗+("OM" ) ⃗) = m(("MO" ) ⃗+("OB" ) ⃗) or, n(-(" a " ) ⃗+("OM" ) ⃗) = m(-("OM" ) ⃗+(" b " ) ⃗) or, –n( "a" ) ⃗ + n("OM" ) ⃗ = –m("OM" ) ⃗ + m( "b" ) ⃗ or, n("OM" ) ⃗ + m("OM" ) ⃗ = m( "b" ) ⃗ + n( "a" ) ⃗ or, ("OM" ) ⃗ (m + n) = m( "b" ) ⃗ + n( "a" ) ⃗ or, ("OM" ) ⃗ = ("m" ( "b" ) ⃗" + n" ( "a" ) ⃗)/"m + n" ∴ Position vector of M = ("OM" ) ⃗ = ("m" ( "b" ) ⃗" + n" ( "a" ) ⃗)/"m + n" Proved.

Theorem 3: Section Formula: External Division

If ( "a" ) ⃗ and ( "b" ) ⃗ be the position vectors of two points A and B respectively and the point P divides the line segment AB externally in the ratio m : n, then the position vector of P is ("m" ( "b" ) ⃗" " -" n" ( "a" ) ⃗)/("m " -" n" ). Proof: Let AB be a line segment and O be the origin. Position vectors of A and B are ("OA" ) ⃗ = ( "a" ) ⃗ and ("OB" ) ⃗ = ( "b" ) ⃗. Suppose, P divides the line segment AB externally in the ratio of m : n. ∴ ("AP" ) ⃗/("BP" ) ⃗ = "m" /"n" or, m("BP" ) ⃗ = n("AP" ) ⃗ or, m(("BO" ) ⃗ + ("OP" ) ⃗) = n(("AO" ) ⃗ + ("OP" ) ⃗) or, m(-("OB" ) ⃗ + ("OP" ) ⃗) = n(-("OA" ) ⃗ + ("OP" ) ⃗) or, m(-(" b " ) ⃗ + ("OP" ) ⃗) = n(-(" a " ) ⃗ + ("OP" ) ⃗) or, –m(" b " ) ⃗ + m("OP" ) ⃗ = –n(" a " ) ⃗ + n("OP" ) ⃗ or, m("OP" ) ⃗ – n("OP" ) ⃗ = m(" b " ) ⃗ – n(" a " ) ⃗ or, ("OP" ) ⃗(m – n) = m(" b " ) ⃗ – n(" a " ) ⃗ or, ("OP" ) ⃗ = ("m" ( "b" ) ⃗" " -" n" ( "a" ) ⃗)/("m " -" n" ) ∴ Position vector of P = ("OP" ) ⃗ = ("m" ( "b" ) ⃗" " -" n" ( "a" ) ⃗)/("m " -" n" ) Proved.

Theorem 4: Centroid Formula

The position vector of the centroid of a triangle is given by ( "g" ) ⃗ = "1" /"3" ((" a " ) ⃗" + " (" b " ) ⃗" + " (" c " ) ⃗ ) where ( "a" ) ⃗, ( "b" ) ⃗ and ( "c" ) ⃗ are the position vectors of the vertices and ( "g" ) ⃗ is the position vector of the centroid. Proof: Let ABC be a triangle and O be the origin. Here, ("OA" ) ⃗ = ( "a" ) ⃗, ("OB" ) ⃗ = ( "b" ) ⃗ and ("OC" ) ⃗ = ( "c" ) ⃗. Let D be the midpoint of AC. Therefore, by midpoint theorem, ("OD" ) ⃗ = "1" /"2" (( "a" ) ⃗ +( "c" ) ⃗ ) Let G be the centroid of the triangle ABC. Then, G divides BD internally in the ratio 2 : 1. Therefore, by section formula, ("OG" ) ⃗ = ("2" ("OD" ) ⃗" + 1" ("OB" ) ⃗)/"2 + 1" = ("2 × " "1" /"2" " " ((" a " ) ⃗" + " (" c " ) ⃗ )" + " (" b " ) ⃗)/"3" = ((" a " ) ⃗" + " (" c " ) ⃗" + " (" b " ) ⃗)/"3" Therefore, position vector of Centroid G = ("OG" ) ⃗ = (" g " ) ⃗ = ((" a " ) ⃗" + " (" b " ) ⃗" + " (" c " ) ⃗)/"3" proved.

Theorem 5:

Prove by vector method that the line joining midpoints of two sides of a triangle is parallel to the third side and half of it. Proof: Let ABC be a triangle and P and Q be the midpoints of the sides AB and AC respectively. ∴ ("PA" ) ⃗ = "1" /"2" ("BA" ) ⃗ and ("AQ" ) ⃗ = "1" /"2" ("AC" ) ⃗ By triangle law of vector addition, ("PQ" ) ⃗ = ("PA" ) ⃗ + ("AQ" ) ⃗ = "1" /"2" ("BA" ) ⃗ + "1" /"2" ("AC" ) ⃗ = "1" /"2" (("BA" ) ⃗ + ("AC" ) ⃗) = "1" /"2" ("BC" ) ⃗ ∴ PQ ∥ BC and PQ = "1" /"2" BC. Proved.

Theorem 6:

Prove by vector method that the line joining vertex and midpoint of the base of an isosceles triangle is perpendicular to the base. Proof: Let ABC be an isosceles triangle where AB = AC and AM is the median to the base BC. Let ("AB" ) ⃗ = ( "a" ) ⃗ and ("AC" ) ⃗ = ( "b" ) ⃗. Then, |( "a" ) ⃗| = |( "b" ) ⃗| i.e. a = b. And, ("BM" ) ⃗ = "1" /"2" ("BC" ) ⃗ By triangle law of vector addition, ("BC" ) ⃗ = ("BA" ) ⃗ + ("AC" ) ⃗ = – ("AB" ) ⃗ + ("AC" ) ⃗ = – (" a " ) ⃗ + (" b " ) ⃗ = ((" b " ) ⃗ – (" a " ) ⃗) ("AM" ) ⃗ = ("AB" ) ⃗ + ("BM" ) ⃗ = ("AB" ) ⃗ + "1" /"2" ("BC" ) ⃗ = (" a " ) ⃗ + "1" /"2" (– (" a " ) ⃗ + (" b " ) ⃗) = ("2" ( "a" ) ⃗ - ( "a" ) ⃗ + ( "b" ) ⃗)/"2" = (( "a" ) ⃗ + ( "b" ) ⃗)/"2" = "1" /"2" ((" a " ) ⃗" +" (" b " ) ⃗ ) Now, ("AM" ) ⃗ . ("BC" ) ⃗ = "1" /"2" ((" a " ) ⃗" +" (" b " ) ⃗ ) . ((" b " ) ⃗ – (" a " ) ⃗) = "1" /"2" (b2 – a2) = 0 [∵ a = b] ∴ AM ⊥ BC proved.

Theorem 7:

Prove by vector method that the quadrilateral joining the midpoints of the adjacent sides of any quadrilateral is a parallelogram. Proof: Let ABCD be a quadrilateral and P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Join BD. From the figure, ("BA" ) ⃗ + ("AD" ) ⃗ = ("BD" ) ⃗ or, 2("PA" ) ⃗ + 2("AS" ) ⃗ = ("BD" ) ⃗ or, 2(("PA" ) ⃗ + ("AS" ) ⃗) = ("BD" ) ⃗ or, ("PA" ) ⃗ + ("AS" ) ⃗ = "1" /"2" ("BD" ) ⃗ or, ("PS" ) ⃗ = "1" /"2" ("BD" ) ⃗ ∴ PS ∥ BD ……….. (i) Again, ("BC" ) ⃗ + ("CD" ) ⃗ = ("BD" ) ⃗ or, 2("QC" ) ⃗ + 2("CR" ) ⃗ = ("BD" ) ⃗ or, 2(("QC" ) ⃗ + ("CR" ) ⃗) = ("BD" ) ⃗ or, ("QC" ) ⃗ + ("CR" ) ⃗ = "1" /"2" ("BD" ) ⃗ or, ("QR" ) ⃗ = "1" /"2" ("BD" ) ⃗ ∴ QR ∥ BD ………. (ii) From (i) and (ii), PS ∥ QR. Similarly by joining AC, we can prove that PQ ∥ SR. Hence PQRS is a parallelogram. Proved.

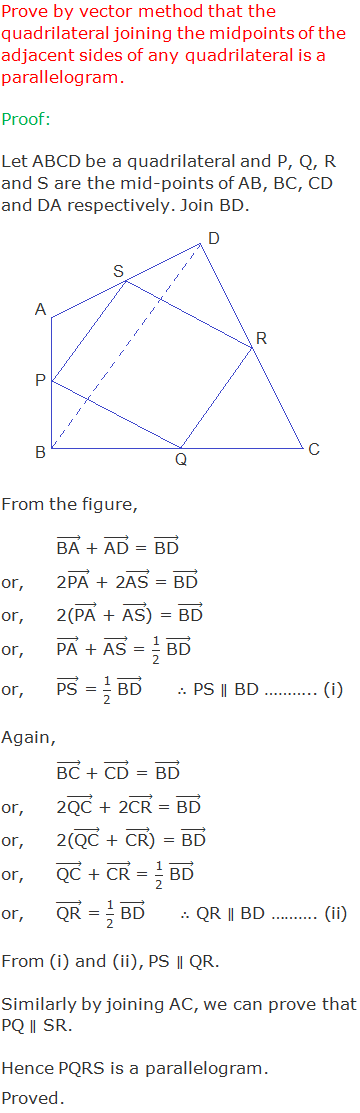
Theorem 8:

Prove by vector method that the diagonals of a parallelogram bisect each other. Proof: Let OACB be a parallelogram and O be the origin. Let, ("OA" ) ⃗ = ( "a" ) ⃗ and ("OB" ) ⃗ = ( "b" ) ⃗. Suppose, M be the middle point of AB. Then by midpoint formula, ("OM" ) ⃗ = "1" /"2" (( "a" ) ⃗+( "b" ) ⃗ ) …………….. (i) Again, let N be the middle point of OC. Then by parallelogram law of vector addition, ("ON" ) ⃗ = "1" /"2" ("OC" ) ⃗ = "1" /"2" (("OA" ) ⃗ + ("OB" ) ⃗) = "1" /"2" (( "a" ) ⃗+( "b" ) ⃗ ) …………….. (ii) From (i) and (ii), M and N have the same position vector. So, they are same point. Hence, the diagonals of a parallelogram bisect each other. Proved.

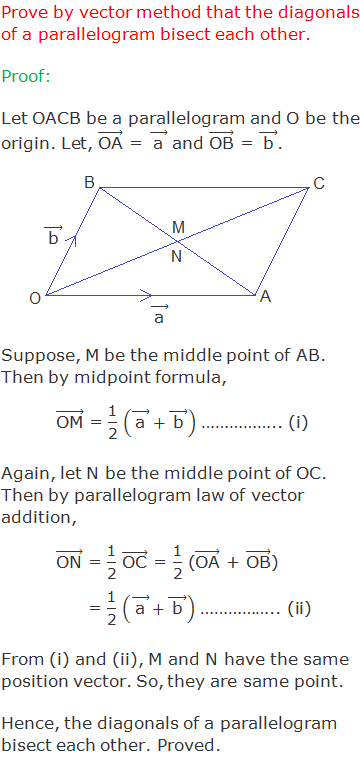
Theorem 9:

Prove by vector method that the diagonals of a rectangle are equal. Proof: Let ABCD be a rectangle and AC and BD are diagonals. Then, ("AB" ) ⃗ = ("DC" ) ⃗, ("AD" ) ⃗ = ("BC" ) ⃗, ∠A = ∠B = ∠C = ∠D = 90° and hence, ("AB" ) ⃗ . ("BC" ) ⃗ = 0 and ("BA" ) ⃗ . ("AD" ) ⃗ = 0. Now, by triangle law of vector addition, ("AC" ) ⃗ = ("AB" ) ⃗ + ("BC" ) ⃗ or, (("AC" ) ⃗)2 = (("AB" ) ⃗ + ("BC" ) ⃗)2 or, AC2 = (("AB" ) ⃗)2 + 2 ("AB" ) ⃗ . ("BC" ) ⃗ + (("BC" ) ⃗)2 or, AC2 = AB2 + 2 × 0 + BC2 or, AC2 = AB2 + BC2 ……………… (i) Again, ("BD" ) ⃗ = ("BA" ) ⃗ + ("AD" ) ⃗ or, (("BD" ) ⃗)2 = (("BA" ) ⃗ + ("AD" ) ⃗)2 or, BD2 = (("BA" ) ⃗)2 + 2 ("BA" ) ⃗ . ("AD" ) ⃗ + (("AD" ) ⃗)2 or, BD2 = BA2 + 2 × 0 + AD2 or, BD2 = BA2 + AD2 or, BD2 = AB2 + BC2 ……………… (ii) From (i) and (ii), AC2 = BD2 ∴ AC = BD Hence the diagonals of a rectangle are equal. Proved.

Theorem 10:

Prove by vector method that the diagonals of a rhombus bisect each other at right angles. Proof: Let OABC is a rhombus, ("OA" ) ⃗ = ("CB" ) ⃗ = (" a " ) ⃗ and ("OC" ) ⃗ = ("AB" ) ⃗ = (" b " ) ⃗ where |(" a " ) ⃗| = |(" b " ) ⃗| i.e. a = b. Let M be the midpoint of diagonal OB and N is the midpoint of diagonal AC. Now, by triangle law of vector addition, ("OB" ) ⃗ = ("OA" ) ⃗ + ("AB" ) ⃗ = (" a " ) ⃗ + (" b " ) ⃗. Since, M is the midpoint of OB, ("OM" ) ⃗ = "1" /"2" ("OB" ) ⃗ = "1" /"2" ((" a " ) ⃗ + (" b " ) ⃗) ………….. (i) Again, since N is the midpoint of AC, by midpoint theorem, ("ON" ) ⃗ = "1" /"2" (("OA" ) ⃗ + ("OC" ) ⃗) = "1" /"2" ((" a " ) ⃗ + (" b " ) ⃗) ………….. (ii) From (i) and (ii), the midpoints M and N of diagonals OB and AC coincide each other, i.e. they are the same point. Hence, the diagonals of a rhombus bisect each other. Now, ("AC" ) ⃗ . ("OB" ) ⃗ = (–( "a" ) ⃗ + ( "b" ) ⃗ ) . (( "a" ) ⃗ + ( "b" ) ⃗) = ((" b " ) ⃗)2 – ((" a " ) ⃗)2 = b2 – a2 = 0 [∵ a = b] ∴ ("AC" ) ⃗ ⊥ ("OB" ) ⃗. Hence diagonals of a rhombus bisect each other at right angle. Proved.

Theorem 11:

Prove by vector method that the angle in the semi-circle is a right angle. Proof: Let O be the centre of a circle and AB be a diameter. ∴ ("AO" ) ⃗ = ("OB" ) ⃗. ∠ACB is an angle in the semi-circle. Join OC. AO = OB = OC (Radii of same circle). By triangle law of vector addition, ("AC" ) ⃗ = ("AO" ) ⃗ + ("OC" ) ⃗ ("CB" ) ⃗ = ("CO" ) ⃗ + ("OB" ) ⃗ = ("CO" ) ⃗ + ("AO" ) ⃗ = ("AO" ) ⃗ – ("OC" ) ⃗ Now, ("AC" ) ⃗ . ("CB" ) ⃗ = ((AO) ⃗+(OC) ⃗ ) . (("AO" ) ⃗ – ("OC" ) ⃗) = (("AO" ) ⃗)2 – (("OC" ) ⃗)2 = AO2 – OC2 = 0 [∵ AO = OC] ∴ ∠ACB = 90°. Proved.

Theorem 12:

Prove by vector method that the midpoint of the hypotenuse of a right angled triangle is equidistant from each vertex. Proof: Let AOC be a right angled triangle and O be the origin. Let ∠AOC = 90° and M is the mid-point of AC. Then, By midpoint theorem, ("OM" ) ⃗ = "1" /"2" (("OA" ) ⃗ + ("OC" ) ⃗) or, 2("OM" ) ⃗ = ("OA" ) ⃗ + ("OC" ) ⃗ or, (2("OM" ) ⃗)2 = (("OA" ) ⃗ + ("OC" ) ⃗)2 or, 4OM2 = (("OA" ) ⃗)2 + 2 ("OA" ) ⃗ . ("OC" ) ⃗ + (("OC" ) ⃗)2 or, 4OM2 = OA2 + 2 × 0 + OC2 or, 4OM2 = OA2 + OC2 = AC2 or, OM2 = "1" /"4" AC2 or, OM = "1" /"2" AC Also, AM = MC = "1" /"2" AC ∴ AM = MC = OM Hence, the midpoint of the hypotenuse of a right angled triangle is equidistant from each vertex. Proved.

Do you have any questions regarding the vector geometry?

You can ask your questions or problems here, in the comment section below.

0 comments:

Subscribe to: Post Comments (Atom)