Transformation: Reflection

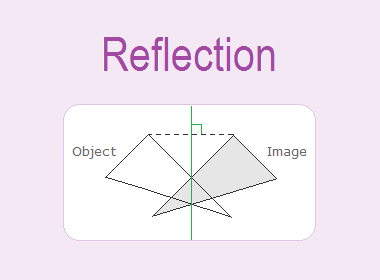
Reflection is a transformation that has a mirror image about a line as a two-way mirror. A line that plays the role of a two-way mirror to give the image of the given objects is called the axis of reflection.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

The following are the properties of reflection:

a.   The object and the image under the reflection are congruent.

b.   The object and the image will be at equal distances from the axis of reflection.

c.   The line joining the object and its image will be perpendicular to the axis of reflection.

Example 1: Find the image of a point P under the reflection over the line AB.

Solution:

To have the image of the point P under the reflection over the line AB, we perform the following steps:

Step 1: Draw PO ⊥ AB.

Step 2: Produce PO upto P’ so that PO = OP’.

The point P’ is called the image of the point P under the reflection over line AB.

 

Example 2: Find the image of quadrilateral PQRS under the reflection over the line AB.

Solution:

Draw perpendicular from each vertex of quadrilateral PQRS on the axis of reflection AB and produce the perpendicular line upto the point whose distance from the axis of reflection is equal to the distance of its object from the axis of reflection as in previous example and join P’Q’R’S’ to get the required image.

 

Example 3: The image of triangle ABC under the reflection is triangle A’B’C’. Find the axis of reflection.

Solution:

Complete the following steps for the axis of reflection.

Step 1: Join any vertex of triangle ABC with its corresponding image. i.e. CC’. (We can join BB’ or AA’ instead)

Step 2: Draw perpendicular bisector of CC’, which is the line of axis of reflection.

∴   MN is the line of axis of reflection.

 

Reflection Using Co-ordinates

The image of geometrical figures under the reflection over a line can easily be obtained with the help of co-ordinates.

Reflection about X-axis

Let A(3, 4) be a point and X-axis be the axis of reflection. From point A draw AM⊥OX and produce AM upto A’ so that AM = AM’ then the co-ordinates of the point A’ will be (3, -4) as shown in the figure.

Hence, A’(3, -4) is the image of the point A(3, 4) under the reflection about X-axis.

Let us see the following table of some points on the plane and their corresponding images under the reflection about X-axis.

From the above table, we can see that the image of any point under the reflection about X-axis is obtained by changing the sign of the y-coordinate of the image point. So we can conclude that the image of a point P(x, y) under the reflection about X-axis is P’(x, -y).

        

Example 4: Find the image of ΔABC with vertices A(2, 3), B(5, 1) and C(3, 5) under the reflection about X-axis. Draw the ΔABC and ΔA’B’C’ (image) on the same graph paper.

Solution:

As the vertices of given triangle ABC are A(2, 3), B(5, 1) and C(3, 5), the vertices of the image ΔA’B’C’ under the reflection about X-axis can be obtained by using formula as follows:

Drawing ΔABC and its image ΔA’B’C’ on the same graph paper, we have the figure as shown.

 

Reflection about Y-axis

Let A(4, -2) be a point and Y-axis be the axis of reflection. From point draw AM⊥OY and produce it upto A’ such that AM = MA’, then the co-ordinates of point A’ will be (-4, -2) as shown in the figure.

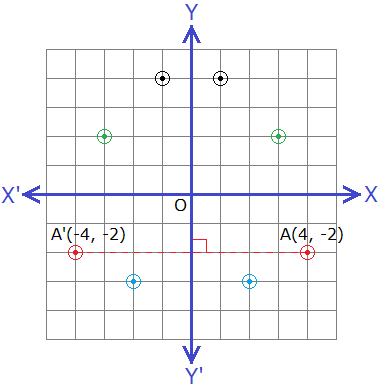
Hence A’(-4, -2) is the image of the point A(4, -2) under the reflection about Y-axis.

        

Let us see the following table of some points on the plane and their corresponding images under the reflection about Y-axis.

From the above table we can see that the image of any point under the reflection about Y-axis is changing by the sign of its x-coordinate from the given point. So we can conclude for the image of a point P(x, y) under the reflection about Y-axis is P’(-x, y).

Example 5: Find the image of quadrilateral PQRS with vertices P(-4, 2), Q(-3, 4), R(1, 5) and S(-2, 1) under the reflection about Y-axis. Draw quadrilateral PQRS and its image P’Q’R’S’ on the same graph paper.

Solution:

As the vertices of given quadrilateral P(-4, 2), Q(-3, 4), R(1, 5) and S(-2, 1), the vertices of the image P’Q’R’S’ can obtain by using the formula (or by drawing on the graph) as follows:

Drawing quadrilateral PQRS and its image P’Q’R’S’ on the same graph paper, we have the figure as shown.

Reflection About the Line y = x

Let, A(1, 5) be a point, and the line y = x be the axis of reflection, the line y = x is a line bisecting the angle between X-axis and Y-axis lying in the first and the third quadrant. Draw a perpendicular AM on the axis of reflection and produce it upto point A’ so that AM = MA’ then the co-ordinates of the point A’ will be (5, 1) as shown in the figure.

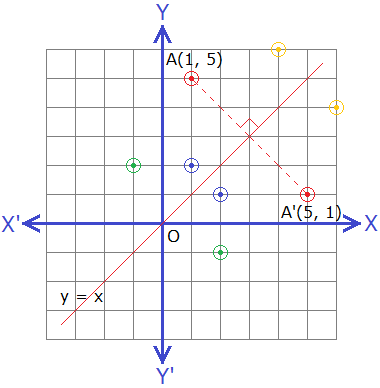
Hence A’(5, 1) is the image of the point A(1, 5) under the reflection about the line y = x.

        

Let us see the following table of some points on the plane and their corresponding images under the reflection about the line y = x.

From the above table we can see that the image of any point under the reflection about the line y = x obtained by interchanging the x-coordinate and y-coordinate of the given point. So we can conclude for the image of a point P(x, y) under the reflection about the line y = x is P’(y, x).

 

Reflection About the line y = -x

Let A(-2, 5) be a point and the line y = -x be the axis of reflection. The line y = -x is a line bisecting the angle between the X-axis and the Y-axis lying in the second and fourth quadrant. From point A draw AM perpendicular on the line y = -x and produce it upto A’ so that AM = MA’, the co-ordinates of A’ is (-5, 2) as shown in the figure.

Hence A’(-5, 2) is the image of the point A(-2, 5) under the reflection about the line y = -x.

        

Let us see the following table of some points on the plane and their corresponding images under the reflection about the line y = -x.

From the above table we can see that the image of any point under the reflection about the line y = -x is obtained by interchanging the x-coordinate and y-coordinate with opposite signs of the given point. So we can conclude for the image of a point P(x, y)under the reflection about the line y = -x is P’(-y, -x).

        

 

Example 6: Find the image of ΔPQR with vertices P(-2, 1), Q(2, 3) and R(-1, 5) under the reflection about the line y = -x. Also draw ΔPQR and its image on the same graph paper.

Solution:

The vertices of given triangle PQR are P(-2, 1), Q(2, 3) and R(-1, 5). The co-ordinates of vertices of the image ΔP’Q’R’ under the reflection about the line y = -x can be obtained by using formula as follows:

Drawing quadrilateral ΔPQR and its image ΔP’Q’R’ on the same graph paper, we have the figure as shown.

 

Reflection About the Line x = a

Let A(1, 2) be a point and the line x = 3 be the axis of reflection. The line x = 3 is a line parallel to Y-axis and at 3 units right from Y-axis. From point A draw AN perpendicular on the line x = 3 and produce it upto A’ so that AN = NA’, then the co-ordinates of A’ is (5, 2) as shown in the figure.

Hence A’(5, 2) is the image of the point A(1, 2) under the reflection about line x = 3.

       

Let us see the following table of some points on the plane and their corresponding images under the reflection about the line x = 3.

From above table we can see that the image of any point under the reflection about the line x = a, is obtained by changing the x-coordinate of the given point by 2a – x. So we can conclude for the image of a point under the reflection about the line x = a.

        

 

Reflection About the line y = b

Let A(2, 1) be a point and the line y = 3 be the axis of reflection. From point A, draw AM perpendicular on the line y = 3 and produce it upto A’ so that AM = MA’, the co-ordinates of point A’ will be (2, 5) as shown in the figure.

Let us see the following table of some points on the plane and their corresponding images under the reflection about the line y = 3.

From the above table we can see that the image of any point is obtained by changing the y-coordinate of the object by 2b – y where b is the distance of the axis of reflection with direction from X-axis. So we can conclude for the image of a point under the reflection about the line y = b.

 

 

Example 7: A(1, 1), B(4, 3) and C(-1, 5) are the vertices of a triangle ABC, find the co-ordinates of the vertices of the image ΔABC under the reflection about the line y = 2.

Solution:

Here A(1, 1), B(4, 3) and C(-1, 5) are the vertices of given triangle. We can find the co-ordinates of the vertices of the image of ΔABC under the reflection about the line y = 2 by using formula.

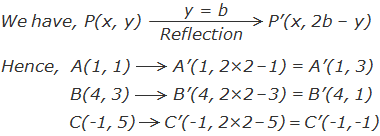
∴   The co-ordinates of the vertices of image ΔA’B’C’ are A’(1, 3), B’(4, 1) and C’(-1, -1) respectively.

Note: We can find these co-ordinates of image ΔA’B’C’ by drawing in graph paper.

 

Conclusion About Reflection Using Co-ordinates:

Do you have any question regarding the reflection using co-ordinates?

 

You can comment your questions or problems here in below.