Cartesian Product

 

If A and B are two non-empty sets then the set of all possible ordered pairs (x, y) such that the first component x is an element of A and the second component y is an element of B is called the Cartesian Product of set A and B. It is denoted by A × B which is read as “A cross B”.

 

In the set-builder form, we can write

A × B = {(a, b): a ∈ A, b ∈ B}

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

For example:

1.     If A = {a, b} and B = {1, 2} then, A × B = {(a, 1), (a, 2), (b, 1), (b, 2)} and B × A = {(1, a), (1, b), (2, a), (2, b)}.

2.     If A = {1, 2, 3} and B = {2, 4, 6} then, A × B = {(1, 2), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 2), (3, 4), (3, 6)} and B × A = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3), (6, 1), (6, 2), (6, 3)}.

3.     If A = {H, T} then A × A = {(H, H), (H, T), (T, H), (T, T)}.

 

Note:

1.     A × B ≠ B × A.

2.     If m = number of elements of A and n = number of elements of B, then the number of elements of A × B is mn.

 

 

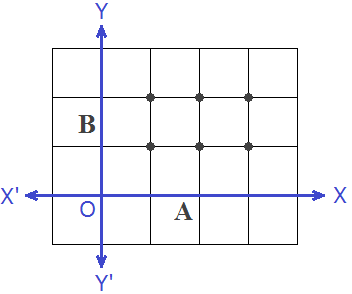
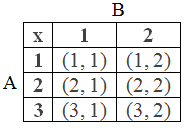
Representation of the Cartesian Product

 

If A = {1, 2, 3} and B = {1, 2} then the Cartesian Product A × B can be represented as follows:

 

(a) Set of Ordered Pairs: A × B = {(1, 1), (1, 2), (2, 1, (2, 2), (3, 1), (3, 2)}

 

(b) Lattice Diagram:

(c) Table:

(d) Mapping Diagram:

(e) Tree Diagram:

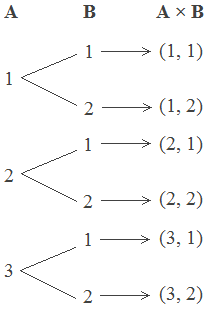
Worked Out Examples

 

Example 1: If A = {a, b} and B = {1, 2, 3} then find A × B.

 

Solution: Here, A = {a, b} and B = {1, 2, 3}

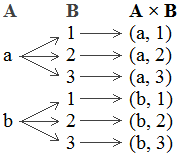
∴ A × B = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)}

 

 

Example 2: If A = {x ∈ N : x ≤ 4}, find A × A.

 

Solution: Here, A = {x ∈ N : x ≤ 4} ∴ A = {1, 2, 3, 4}

Now, from the above table

A × B = {(1, 1), (a, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}

 

 

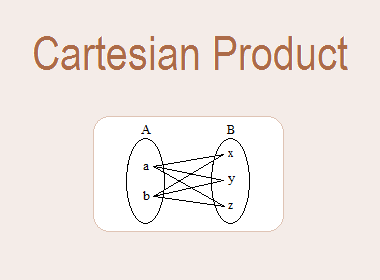
Example 3: Draw the arrow diagram of A × B and B × A if A = {a, b} and B = {x, y, z}.

 

Solution: Here, A = {a, b} and B = {x, y, z}

 

A × B in mapping diagram

A × B = {(a, x), (a, y), (a, z), (b, x), (b, y), (b, z)}

 

B × A in mapping diagram

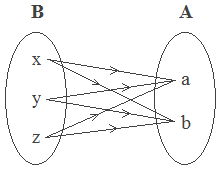
B × A = {(x, a), (x, b), (y, a), (y, b), (z, a), (z, b)}