Relation

 

If A and B are two non-empty sets then any subset of ordered pairs of a cartesian product A × B is called a relation from set A to set B. A relation is denoted by xRy or simply R, if (x, y) ∈ R. A relation from set A to A is called a relation on A.

 

Ways of Representing a Relation

 

Relations can be expressed in various ways. Here are some examples:

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Examples:

1. By specifying or displaying a set of ordered pairs:

    (a) R = {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25)}

    (b) R = {(1, 1), (2, 2), (3, 3)}

2. By standard description, using a rule or a formula:

    (a) Let A = {1, 2, 3} and B = {1, 4, 9}. R = {(x, y): y = x²}. Then R = {(1, 1), (2, 4), (3, 9)}.

    (b) Let A = {1, 2, 3} and B = {1, 2, 3}. R = {(x, y): x = y}. Then R = {(1, 1), (2, 2), (3, 3)}

 

3. By table, such as:

    (a) R = {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25)}

    (b) R = {(1, 1), (2, 2), (3, 3)}

4. By arrow diagram:

    

R = {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25)}

 

5. By graphs:

    

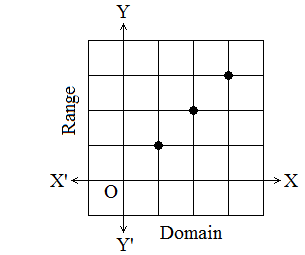
R = {(1, 1), (2, 2), (3, 3)}

 

Domain and Range of a Relation

 

The domain of a relation is the set of all the first elements of the ordered pairs of R, and its range is the set of all second elements.

 

Examples:

1. Let R₁ = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}

    Domain of R₁ = {1, 2, 3}

    Range of R₁ = {1, 2, 3}

 

2. Let R₂ = {(1, 2), (3, 4), (5, 6)}

    Domain of R₂ = {1, 3, 5}

    Range of R₂ = {2, 4, 6}

 

 

Types of Relation

 

Let us consider A = {1, 2, 3}

 

Then the cartesian product A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}

 

(i)             Reflexive Relation

A relation R is called reflexive if every element of the relation is related to itself. It is written as xRx. For example: R₁ = {(1, 1), (2, 2), (3, 3)}

(ii)          Symmetric Relation

In a relation, if the first and second components of the ordered pairs are interchanged, the relation still holds. It is called the symmetric relation. For example: R₂ = {(1, 2), (2, 1)}. It is written as if xRy then yRx. If x = y then the relation is Anti-symmetric. e.g. R₃ = {(1, 2), (1, 3), (2, 1), (3, 1)}

(iii)        Transitive Relation

A relation R is called transitive if aRb and bRc gives aRc. Thus, if a is related to b and b is related to c then a is related to c. For example: R₃ = {(1, 2), (2, 3), (1, 3)}.

(iv)        Equivalence Relation

A relation is called equivalence if and only if it is reflexive, symmetric and transitive. For example: R₄ = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 1), (2, 3), (3, 2), (3, 1)}

 

 

Inverse Relation

 

A relation obtained by interchanging the first and second elements in the ordered pairs of a relation is known as the inverse of the given relation. If R denotes a given relation its inverse is denoted by R^-1.

 

In symbols, if R = {(a, b): a ∈ A, b ∈ B}, then R^-1 = {(b, a): b ∈ B, a ∈ A}.

 

 

Worked Out Examples

 

Example 1: Let A = {1, 2, 3, 4} and B = {1, 3, 5}. Find the relation R from A to B determined by the condition ‘x < y’.

 

Solution: Here,

A = {1, 2, 3, 4} and B = {1, 3, 5}

Since x ∈ A, y ∈ B and x < y, R = {(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}

 

 

Example 2: Find the domain, range and inverse of the relation R = {(1, 2), (2, 4), (3, 6), (4, 8)}.

 

Solution: Here,

R = {(1, 2), (2, 4), (3, 6), (4, 8)}

Domain of R = {1, 2, 3, 4}

Range of R = {2, 4, 6, 8}

R^-1 = {(2, 1), (4, 2), (6, 3), (8, 4)}

 

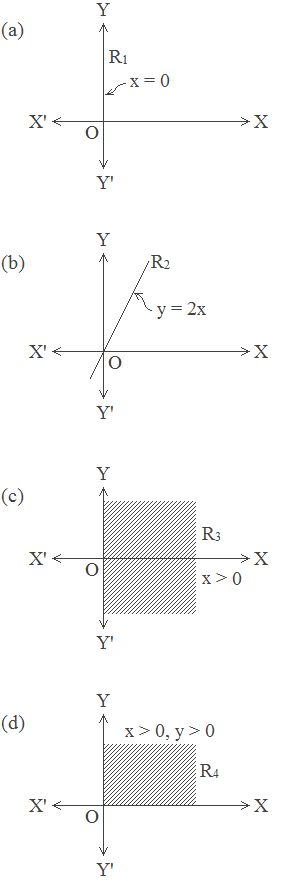
Example 3: In the universe R × R (R is the set of all real numbers), graph (or sketch) the relations expressed below:

(a) R₁ = {(x, y) : x = 0}

(b)R₂ = {(x, y) : y = 2x}

(c) R₃ = {(x, y) : x < 0}

(d)R₄ = {(x, y) : x > 0, y > 0}

 

Solution:

The graph of R₁, R₂, R₃ and R₄ are shown in figures a, b, c, and d respectively.