Triangle Theorems

0 comments

Triangle Theorems

 

Theorem is a geometrical statement which is true and can be proved by using known facts and axioms. Generally, we prove geometrical theorems by two methods, one method is experimental verification and another method is theoretical proof.


 

Some of the triangle theorems and their experimental verification and/or theoretical proofs are given below:



********************


10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.


Install Quick Math Solver

********************


Install 10 Math Problems

******************** 

 


Theorem 1:

“Among the straight lines drawn from an external point to a given straight line, the perpendicular is the shortest one.”

 

 

Experimental Verification

 

PA, PB, PM and PN are the straight lines drawn from a point P to the line XY and PA⊥XY. Three such figures are drawn with the help of scale, pencil and protractor.


Figure for experimental verification of theorem 1.

Table,

Table 1

Conclusion: It is experimentally verified that the perpendicular drawn from a point to the straight lines is the shortest distance from the point to the line.


 

Theorem 2:

“The sum of two sides of a triangle is greater than the third side.”

 

 

Experimental Verification

 

Three triangles ABC of different shapes and sizes are drawn with the help of scale and pencil.


Figure for experimental verification of theorem 2.

Table,

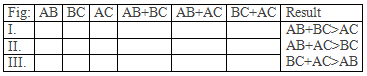
Table 2

Conclusion: It is experimentally verified that the sum of two sides of a triangle is greater than the third side.

 

 

Theorem 3:

“In a triangle, the side opposite to the greater angle is longer than the side opposite to the smaller angle.”

 

 

Experimental Verification

 

Three triangles PQR of different shapes and sizes with ∠P greater than other angles ∠Q and ∠R are drawn with the help of scale and pencil.


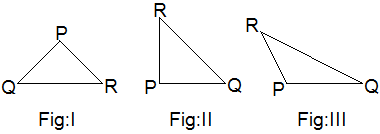
Figure for experimental verification of theorem 3.

Table,

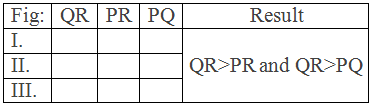
Table 3

Conclusion: Hence it is experimentally verified that the side opposite to greater angle is longer than the side opposite to smaller angle.

 

 

Theorem 4:

 “The sum of three angles of a triangle is equal to two right angles.”

 

 

Experimental Verification

 

Three triangles ABC of different shapes and sizes are drawn with the help of scale and pencil.


Figure for experimental verification of theorem 4.

Table,

Table 4

Conclusion: Hence it is experimentally verified that the sum of the angles of a triangle is two right angles.

 

 

Theoretical Proof:


Figure for theoretical proof of theorem 4.

Given: ABC is a triangle.

To prove: ∠ABC+∠BAC+∠ACB = 180°

Construction: Through A, PQ parallel to BC is drawn.

 

Proof:

Statements                 Reasons

1. ∠PAB = ∠ABC ------> Alternate angles

2. ∠QAC = ∠ACB -------> Alternate angles

3. ∠PAB+∠BAC+∠QAC = 180° -----> Straight angle

4. ∠ABC+∠BAC+∠ACB = 180° -----> From statements 1, 2 and 3.

Proved.

 

 

Theorem 5:

“The exterior angle of a triangle is equal to the sum of the two interior opposite angles.”

 

 

Experimental Verification

 

Three triangles PQR with exterior angle ∠PRS are drawn with the help of scale and pencil.


Figure for experimental verification of theorem 5.

Table,

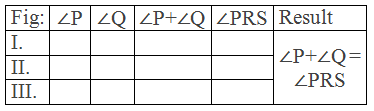
Table 5

Conclusion: Hence it is experimentally verified that the exterior angle of a triangle is equal to the sum of the two interior opposite angles.

 

 

Theoretical Proof:


Figure for theoretical proof of theorem 5.

Given: In ∆ABC, ∠ACD is an exterior angle.

To prove: ∠ACD = ∠A + ∠B

 

Proof:

Statements                            Reasons

1. ∠ACB + ∠ACD = 180° -----> Straight angle.

2. ∠A+∠B+∠ACB = 180° -----> Sum of angles of a ∆.

3. ∠ACB+∠ACD = ∠A+∠B+∠ACB -----> From statements 1 and 2.

4. ∠ACD = ∠A+∠B ------> Removing ∠ACB from both sides.

Proved.

 

 

Theorem 6:

“Base angles of an isosceles triangle are equal.” OR “If two sides of a triangle are equal, then the angles opposite to them are also equal.”

 

 

Experimental Verification

 

Three isosceles triangles PQR of different shapes and sizes with PQ = PR are drawn with the help of scale, pencil and compass.


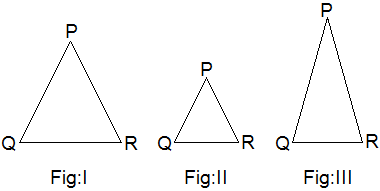
Figure for experimental verification of theorem 6.

Table,

Table 6

Conclusion: Hence it is experimentally verified that if two sides of a triangle are equal then the angles opposite to them are also equal.

 

 

Theoretical Proof:


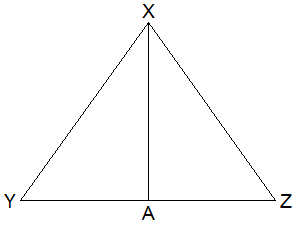
Figure for theoretical proof of theorem 6.

Given: ∆XYZ is an isosceles triangle in which XY = XZ.

To prove: ∠XYZ = ∠YZX

Construction: XA⊥YZ drawn.

 

Proof:

Statements                           Reasons

1. In ∆XYA and ∆XZA

     i.   ∠XAY = ∠XAZ (R) ------> Both right angles.

     ii.  XY = XZ (H) ------> Given.

     iii. XA = XA (S) ------> Common side.

2. ∆XYA ≅ ∆XZA ------> By RHS axiom.

3. ∠XYA = ∠XZA -----> Corresponding angles of congruent triangles

4. ∠XYZ = ∠YZX -----> From statement 3.

Proved.

 

 

Theorem 7:

“In a triangle, the sides opposite to the equal angles are also equal.”

 

 

Experimental Verification

 

Three triangles PQR of different shapes and sizes with ∠Q = ∠R are drawn with the help of scale, pencil and protractor.


Figure for experimental verification of theorem 7.

Table,

Table 7

Conclusion: Hence it is experimentally verified that the sides opposite to equal angles in a triangle are equal.

 

 

Theoretical Proof:


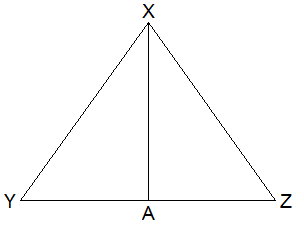
Figure for theoretical proof of theorem 7.

Given: In ∆XYZ, ∠Y = ∠Z.

To prove: XY = XZ

Construction: XA⊥YZ drawn.

 

Proof:

Statements                  Reasons

1. In ∆XYA and ∆XZA

     i. XA = XA (S) -------> Common side.

     ii. ∠XAY = ∠XAZ (A) -------> Both right angles.

     iii. ∠Y = ∠Z (A) -------> Given.

2. ∆XYA ≅ ∆XZA -------> By SAA axiom.

3. XY = XZ -------> Corresponding sides of congruent triangles.

Proved.

 

 

Theorem 8:

“The bisector of the vertical angle of an isosceles triangle is perpendicular to the base and bisects the base.”

 

 

Experimental Verification

 

Three triangles PQR with bisector PX of different shapes and sizes are drawn with the help of scale, pencil and compass.


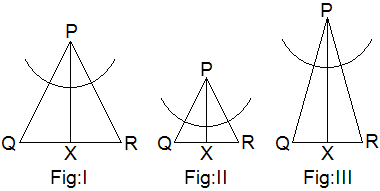
Figure for experimental verification of theorem 8.

Table,

Table 8

Conclusion: Hence it is experimentally verified that the bisector of vertical angle of an isosceles triangle is perpendicular to the base and bisects the base.

 

 

Theoretical Proof:


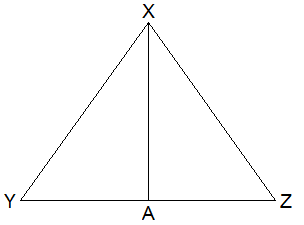
Figure for theoretical proof of theorem 8.

Given: ∆XYZ is an isosceles triangle in which XY = XZ. XA is bisector of ∠YXZ i.e. ∠AXY = ∠AXZ.

To prove: XA⊥YZ and YA = ZA

 

Proof:

Statements                  Reasons

1. In ∆XYA and ∆XZA

     i. XY = XZ (S) -------> Given.

     ii. ∠AXY = ∠AXZ (A) -------> Given.

     iii. XA = XA (S) -------> Common side.

2. ∆XYA ≅ ∆XZA -------> By SAS axiom.

3. ∠XAY = ∠XAZ -------> Corresponding angles of congruent triangles.

4. XA⊥YZ -------> Being adjacent angles equal (statement 3).

5. YA = ZA ------> Corresponding sides of congruent triangles.

Proved.

 

 

Theorem 9:

“The line joining the mid-points of the base of an isosceles triangle to the opposite vertex is perpendicular to the base and bisects the vertical angle.”

 

 

Experimental Verification

 

Three triangles PQR with A as mid-point of QR of different shapes and sizes are drawn with the help of scale, pencil and compass.


Figure for experimental verification of theorem 9.

Table,

Table 9

Conclusion: Hence it is experimentally verified that the line joining mid-point of the base of an isosceles triangle to the opposite vertex is perpendicular to the base and bisects the vertical angle.

 

 

Theoretical Proof:


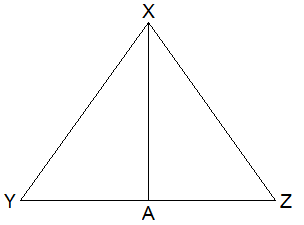
Figure for theoretical proof of theorem 9.

Given: ∆XYZ is an isosceles triangle in which XY = XZ. A is the mid-point of YZ i.e. AY = AZ.

To prove: XA⊥YZ and ∠AXY = ∠AXZ

 

Proof:

Statements                     Reasons

1. In ∆XYA and ∆XZA

     i.   XY = XZ (S) --------> Given.

     ii.  AY = AZ (S) --------> Given.

     iii. XA = XA (S) -------> Common side.

2. ∆XYA ≅ ∆XZA --------> By SSS axiom.

3. ∠XAY = ∠XAZ -------> Corresponding angles of congruent triangles.

4. XA⊥YZ -------> Being adjacent angles equal (statement 3).

5. ∠AXY = ∠AXZ -------> Corresponding angles of congruent triangles.

Proved.

 

 

Theorem 10:

“A line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of its length.”

 

 

Experimental Verification

 

Three triangles ABC with X and Y mid-points of AB and AC respectively of different shapes and sizes are drawn with the help of scale, pencil and compass.


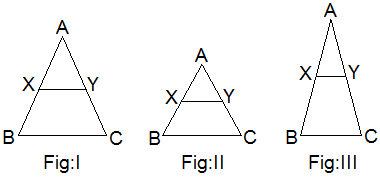
Figure for experimental verification of theorem 10.

Table,

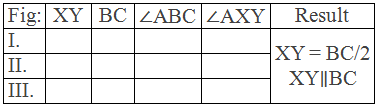
Table 10

Conclusion: Hence it is experimentally verified that a line segment joining the mid-points of any two sides of a triangle is parallel to third side and is equal to half of its length.

 

 

Theoretical Proof:


Figure for theoretical proof of theorem 10.

Given: ABC is a triangle in which AX = XB and AY =YC.

To prove: XY∥BC and XY = BC/2

Construction: CZ is drawn such that it is parallel to BX and XY is produced to meet at Z.

 

Proof:

Statements                             Reasons

1. In ∆AXY and ∆YCZ

     i.   ∠XYA = ∠ZYC (A) --------> VOA.

     ii.  AY = YC (S) -------> Given.

     iii. ∠XAY = ∠ZCY (A) --------> Alternate angles.

2. ∆AXY ≅ ∆YCZ --------> By ASA axiom.

3. AX = CZ --------> Corresponding sides of congruent triangles.

4. AX = BX --------> Given.

5. CZ = BX -------> From statements 3 and 4.

6. CZ ∥ BX --------> By construction.

7. XBCZ is a parallelogram. ------> Being opposite sides equal and parallel (5. And 6.)

8. XY = YZ i.e. XY = XZ/2 ------> Corresponding sides of congruent triangles.

9. XZ∥BC and XZ = BC -------> Opposite sides of a parallelogram.

10. XY∥BC and XY = BC/2 -------> From Statements 9 and 8.

Proved.

 


 

Labels:

0 comments:

Subscribe to: Post Comments (Atom)