Function

 

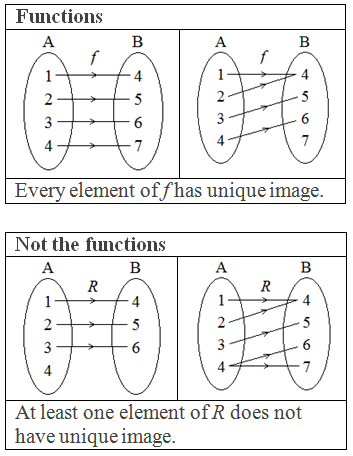
Consider two sets A and B. Any non-empty subset R of the cartesian product A × B is called a relation from A to B. A special type of relation associates each element of set A with the one and only element of B. This is indeed a refinement of the concept of relation. Such a refinement is known as a function. We may define a function in the following way:

 

A function from a set A to a set B is a relation (or rule) which associates each element of A with a unique element of B.

 

Symbolically, we write

 

f : A → B

 

to mean “f is a function from A to B”. Further, an element y of B associated with an element x of A is denoted by f(x). Equivalently, we write y = f(x) which reads ‘y equals f of x’. Here f(x) is known as the image of f at x or the value of f at x.

 

The letters f, g, h, F, G, H, φ etc. are reserved for denoting functions.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

******************** 

 

Representation of Functions

 

The various ways by which a function can be represented are mentioned below:

(i) A table

(ii) A set of ordered pairs

(iii) An arrow diagram

(iv) A graph

(v) A machine

(vi) A formula

 

Example: Let A = {1, 2, 3} and B = {1, 4, 9}. And a function assigns each number of A with its square in B. So, f(1) = 1, f(2) = 4 and f(3) = 9. Here, the domain of the definition of f is A and the range of f is f(A) = B.

 

This function f : A → B can be represented by

 

(a) A table:

(b) A set of ordered pairs:

f = {(1, 1), (2, 4), (3, 9)}

 

(c) An arrow diagram:

(d) A graph:

(e) A machine:

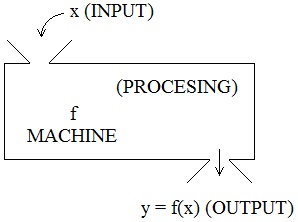
(f) A formula:

y = f(x) = x², where x ∈ A and y ∈ B.

 

 

Testing of Function

 

We can test whether a given relation is a function or not by applying the following tests.

 

(i) If a function is in the form of a set of ordered pairs, examine whether the first element of all the ordered pairs are different or not. If not, it is not a function.

(ii) In the arrow diagram, examine whether each element of the first set has only one image in the second set or not. If not, it is not a function.

(iii) Vertical Line Test: In the graph of a relation, it will represent a function if each vertical line cuts the graph at only one point. The graph will not represent a function if a vertical line cuts the graph at more than one point.

 

Domain, Range, and Co-domain of a Function

 

If f is a function from set A to set B i.e. f : A → B then set A is said to be the domain of f and B, the co-domain of f. The set of elements of B which are the images of the elements of A is known as the range of f.

 

The image of a function is the set of all output values it may produce. For a given function, the set of all elements of the domain that are mapped into a given subset of co-domain (Range) is known as the pre-images and the elements of the range are called images.

  

Types of Functions

 

Onto Function:

A function f is called an onto function if its range and co-domain are equal.

 

Into Function:

A function f is said to be an into function if its range is a proper subset of its co-domain.

 

One to one Function:

A function f is called one to one function if every element in the range has a single pre-image.

 

Many to one Function:

A function f is called many to one function if at least one element of the range has more than one pre-image.

 

Value of a Function

 

If f is a function and (p, q) is in f then we write f(p) = q, where f(p) is called the value of the function at p.

 

 

Worked Out Examples

 

Example 1: Let A = {1, 2, 3}, B = {2, 4, 6} and f : A → B such that f(1) = 2, f(2) = 4 and f(3) = 6. Represent the function f by

(i) Tabular form

(ii) Set of ordered pairs

(iii) Arrow diagram

(iv) Graph

(v) Formula (an equation)

 

Solution: Here,

A = {1, 2, 3}

B = {2, 4, 6}

f : A → B

(i) In a tabular form:

f(1) = 2       i.e. when x = 1 then y = 2

f(2) = 4       i.e. when x = 2 then y = 4

f(3) = 6       i.e. when x = 3 then y = 6

(ii) A set of ordered pairs form:

f = {(1, 2), (2, 4), (3, 6)}

 

(iii) In an arrow diagram:

1 corresponds with f(1) = 2

2 corresponds with f(2) = 4

3 corresponds with f(3) = 6

(iv) In a graph:

The points with ordered pairs: (1, 2), (2, 4), (3, 6) are plotted.

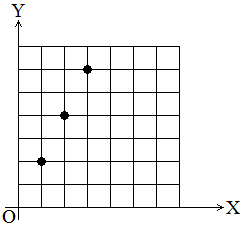
(v) In formula (an equation):

When x = 1 then y = f(1) = 2 = 2 × 1

When x = 2 then y = f(2) = 4 = 2 × 2

When x = 3 then y = f(3) = 6 = 2 × 3

∴ The function f can be expressed as y = 2x or f(x) = 2x.

 

Example 2: What element in the domain has image 9 under the function f(x) = 4x + 5?

 

Solution: Here,

f(x) = 4x + 5 and image of f = 9

So, f(x) = 9

or, 4x + 5 = 9

or, 4x = 9 – 5

or, 4x = 4

or, x = 4/4

or, x = 1

Thus, the required element of the domain is 1.

 

 

Example 3: If a function f is such that f(x + 5) = f(x) + f(5), x ∈ R, show that f(0) = 0 and f(-5) = - f(5).

 

Solution: Here,

f(x + 5) = f(x) + f(5)

at x = 0

f(0 + 5) = f(0) + f(5)

or, f(5) = f(0) + f(5)

or, f(5) – f(5) = f(0)

or, 0 = f(0)

∴ f(0) = 0

 

Again, at x = -5

f(-5 + 5) = f(-5) + f(5)

or, f(0) = f(-5) + f(5)

or, 0 = f(-5) + f(5)

or, -f(5) = f(-5)

∴ f(-5) = -f(5) proved.

 

 

Example 4: A function f is defined by f(x) = x² + 4x + 5 then find the value of

(i) f(5)

(ii) f(-2)

(iii) f(8) + f(9)

 

Solution: Here,

f(x) = x² + 4x + 5

(i) When x = 5 then, f(5) = 5² + 4×5 + 5 = 25 + 20 + 5 = 50

(ii) When x = -2 then f(-2) = (-2)² + 4 × (-2) + 5 = 4 – 8 + 5 = 1

(iii) When x = 8 then f(8) = 8² + 4×8 + 5 = 64 + 32 + 5 = 101

When x = 9 then f(9) = 9² + 4×9 + 5 = 81 + 36 + 5 = 122

Now, f(8) + f(9) = 101 + 122 = 223

 

 

Example 5: Let A = {a, b, c}, B = {5, 7, 10, 12} and define f(a) = 5, f(b) = 7, f(c) = 10. Identify whether function f : A → B is into or onto.

 

Solution: Here,

f(a) = 5, f(b) = 7 and f(c) = 10

Range = {5, 7, 10}

Co-domain = {5, 7, 10, 12}

The range is a proper subset of the co-domain. Thus the given function is an into function.

 

Example 6: Let the function f : N → N be defined by f(x) = 2x + 1

(i) Is the function f onto?

(ii) What is the range of 8?

(iii) What is the pre-image of 11?

(iv) If (k, 4k – 5) lies in the function, find the value of k.

 

Solution: Here,

(i)

Domain = {1, 2, 3, …………..}

Range = {1, 2, 3, …………….}

y = f(x) = 2x + 1

When x = 1 then y = 2×1 + 1 = 3

When x = 2 then y = 2×2 + 1 = 5

When x = 3 then y = 2×3 + 1 = 7

∴ Range = {3, 5, 7, ………….} ≠ Co-domain of f

Thus, f is not an onto function.

 

(ii)

When x = 8 then y = 2×8 + 1 = 17

Thus, the image of 8 is 17.

 

(iii)

For pre-image of 11, f(x) = 11

or, 2x + 1 = 11

or, 2x = 11 – 1

or, x = 10/2

or, x = 5

∴ The pre-image of 11 is 5.

 

(iv)

(k, 4k – 5) lies on f(x) = 2x + 1

So, x = k and f(x) = 4k – 5

Now, f(x) = 2x + 1

or, 4k – 5 = 2k + 1

or, 4k – 2k = 1 + 5

or, 2k = 6

or, k = 3

∴ The value of k is 3.

 

 

Example 7: If f(x) and g(x) be two functions defined by f(x) = 4x² – 3x + 4 and g(x) = 3x² – 7x + 9 such that f(x) = g(x). Find the value of x.

 

Solution: Here,

f(x) = g(x)

or, 4x² – 3x + 4 = 3x² – 7x + 9

or, 4x² – 3x + 4 – 3x² + 7x – 9 = 0

or, x² + 4x – 5 = 0

or, x² + 5x – x – 5 = 0

or, x(x + 5) – 1(x + 5) = 0

or, (x + 5)(x – 1) = 0

∴ Either: x + 5 = 0 or x = -5

Or: x – 1 = 0 or, x = 1

∴ x = -5, 1

Thus, the value of x are -5 and 1.