Geometric Mean (GM)

 

If three numbers a, b and c are in geometric progression GP, then the middle term b is known as the geometric mean (GM) between the other two. For example, 24, 12 and 6 are in GP, so 12 is the geometric mean between 24 and 6.

 

If any number of terms are in GP, then the terms between the first and the last terms are known as the geometric means between the first and the last. For example, 1, 2, 4, 8, 16, 32 are in GP and 2, 4, 8, 16 are the geometric means between 1 and 32.

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

******************** 

 

Geometric Mean Between Two Numbers

 

Let G be the geometric mean between two numbers a and b then a, G, b are in GP.

 

Now by definition,

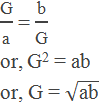
Example 1: Find the geometric mean between 2 and 8.

 

Solution:

 

Here,

The first term (a) = 2

Last term (b) = 8

Geometric mean (G) = ?

 

We know,

Geometric Means Between Two Numbers

 

Let x₁, x₂, … … …, x_n1 be the n₁ geometric means between a and b, then a, x₁, x₂, x₃, … … …, x_n1, b are in GP. If r be the common ratio, then t_n = ar^n-1

 

As there are n₁ + 2 terms in all i.e. n = n₁ + 2

 

or, b = ar^n1+2-1

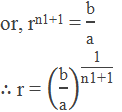
Now, the required geometric means are

x₁ = ar

x₂ = ar²

x₃ = ar³

x_n = arⁿ

 

Note: The second term of the sequence is the first mean and the third term is the second mean and so on.

 

 

Example 2: Insert 5 geometric mean between 81 and 3.

 

Solution:

 

Here,

The first term (a) = 81

The last term (b) = 3

No. of means (n1) = 5

 

Hence the common ratio,

Therefore, geometric means are:

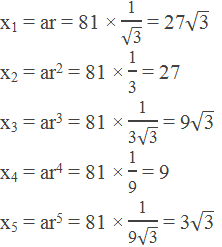
Example 3: If 4, p, q, - 1/16 are in GP, find p and q.

 

Solution:

 

Here,

First term (a) = 4

Last term (b) = - 1/16

n₁ = no. of means = 2

Example 4: Two numbers are in ratio 16:1 and their GM is 16. Find the numbers.

 

Solution:

 

Let the two numbers be 16x and x and their GM is 16.

or, (16)² = 16x × x

256 = 16x²

or, x² = 16

or, x = ±4

 

When x = 4, the numbers are 4x and x i.e. 64 and 4.

When x = -4, the numbers are 4x and x i.e. -64 and -4.

 

 

Example 5: Find the number of GM’s inserted between 4 and 128, the ratio of the first mean and the last mean is 1:8.

 

Solution:

 

Here,

The first term (a) = 4

The last term (b) = 128

Let the number of means = n

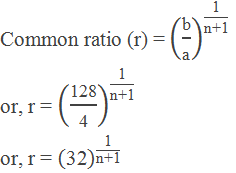
From the question, First mean : Last mean = 1 : 8

or, 5 – 5n = -3n – 3

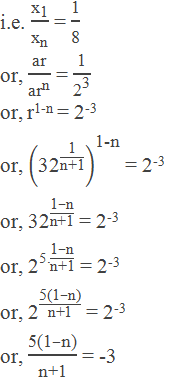
or, -5n + 3n = -3 – 5

or, -2n = -8

or, n = 4

 

 

Relation Between AM and GM of two Positive Numbers

 

Let a and b be two positive numbers and AM and GM be the arithmetic mean and geometric mean between a and b respectively, then

 

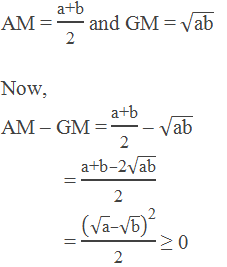
Hence, AM ≥ GM

 

Therefore the arithmetic mean between two positive numbers is greater than or equal to their geometric mean.

 

Example 6: Find the two numbers whose AM is 25 and GM is 20.

 

Solution:

 

Let the two numbers be a and b, then

∴ a – b = 30 ……………… (iii)

 

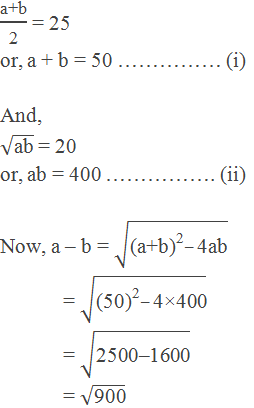
Solving equations (i) and (iii), we get

a = 40 and b = 10

 

Hence, the required numbers are 40 and 10.