Sum of Geometric Series

 

The series associated with a geometric sequence is known as a geometric series. For example, 2 + 4 + 8 + 16 + 32 is the geometric series associated with the geometric sequence 2, 4, 8, 16, 32.

 

Let a be the first term, r be the common ratio, n be the number of terms, l be the last term and S_n be the sum to n terms of GS, then

 

S_n = a + ar + ar² + … … … + ar^n-2 + ar^n-1 ………. (i)

 

Multiplying both sides by r,

 

rS_n = ar + ar² + ar³ + … … … + ar^n-1 + arⁿ …….. (ii)

 

Subtracting (i) from (ii), we get

 

(r – 1)S_n = -a + arⁿ

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Worked Out Example

 

Example 1: Find the sum of the geometric series 1 + 2 + 4 + … … … 7 terms.

 

Solution:

 

Here,

 

First term (a) = 1

Common ratio (r) = 2/1 = 2

Number of terms (n) = 7

Sum of the terms (S_n) = ?

 

By using formula,

 

∴ S_n = 127

 

Example 2: In a GP, the first term is 7, the last term is 448 and the sum is 889, find the common ratio.

 

Solution:

 

Here,

 

First term (a) = 7

Last term (l) = 448

Sum of terms (S_n) = 889

Common ratio (r) = ?

 

By using the formula,

 

∴ The common ratio is 2.

 

 

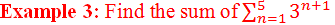
Solution:

 

Here,

 

= 3¹⁺¹ + 3²⁺¹ + 3³⁺¹ + 3⁴⁺¹ + 3⁵⁺¹

= 3² + 3³ + 3⁴ + 3⁵ + 3⁶

= 9 + 27 + 81 + 243 + 729

= 1089

 

 

Example 4: How many terms of the series 32 + 48 + 72 + … … will add upto 665?

 

Solution:

 

Here,

 

First term (a) = 32

Common ratio (r) = 48/32 = 3/2

Sum of terms (S_n) = 665

Number of terms (n) = ?

 

By using formula,

∴ n = 6

 

∴ The number of terms = 6

 

 

Example 5: If S₃ and S₆ of a GS are 7 and 63 respectively, find the common ratio.

 

Solution:

 

Here,

 

or, r³ + 1 = 9

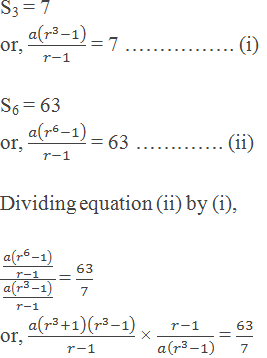
or, r³ = 9 – 1

or, r³ = 8

or, r³ = 2³

or, r = 2

 

∴ Common ratio = 2

 

 

Example 6: The second and fifth terms of GS are 3 and 81 respectively. Find the sum of the first five terms.

 

Solution:

 

Here,

 

The second term of GS is 3

i.e. t₂ = 3

or, ar = 3

 

Again, the fifth term of GS is 81

i.e. t₅ = 81

or, ar⁴ = 81

or, ar.r³ = 81

or, 3.r³ = 81

or, r³ = 81/3

or, r³ = 27 = 3³

or, r = 3

 

And, ar = 3

or, a×3 = 3

or, a = 1

 

Now,

 

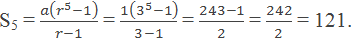
Example 7: Find the GP for which the sum of the first two terms is -4 and the fifth term is 4 times the third term.

 

Solution:

 

Here,

 

S₂ = -4

i.e. t₁ + t₂ = -4

or, a + ar = -4

or, a(1 + r) = -4 ……………… (i)

 

t₅ = 4 × t₃

i.e. ar⁴ = 4 × ar²

or, r² = 4

or, r = ±2

 

Taking r = 2, from equation (i), we have

a(1 + 2) = -4

or, a = -4/3

 

The GP is a, ar, ar², …

i.e. -4/3, -4×2/3, -4×22/3, …

i.e. -4/3, -8/3, -16/3, …

 

Taking r = -2, from equation (i), we have

a(1 – 2) = -4

or, a = 4

 

The GP is a, ar, ar², …

i.e. 4, 4×-2, 4×(-2)², …

i.e. 4, -8, 16, …

 

Example 8: If the sum of the first three terms of a GP is 1 and the sum of the first six terms is 28. Find the sum of the first 9 terms of the series.

 

Solution:

 

Here,

 

or, r³ + 1 = 28

or, r³ = 28 – 1

or, r³ = 27

or, r³ = 3³

or, r = 3

 

 

∴ The sum of first 9 terms is 757.