Factors of 74

 

The factors of 74 are 1, 2, 37, and 74 i.e. F₇₄ = {1, 2, 37, 74}. The factors of 74 are all the numbers that can divide 74 without leaving a remainder.

 

We can check if these numbers are factors of 74 by dividing 74 by each of them. If the result is a whole number, then the number is a factor of 74. Let's do this for each of the numbers listed above:

 

·        1 is a factor of 74 because 74 divided by 1 is 74.

·        2 is a factor of 74 because 74 divided by 2 is 37.

·        37 is a factor of 74 because 74 divided by 37 is 2.

·        74 is a factor of 74 because 74 divided by 74 is 1.

 

 

How to Find Factors of 74?

 

1 and the number itself are the factors of every number. So, 1 and 74 are two factors of 74. To find the other factors of 74, we can start by dividing 74 by the numbers between 1 and 74. If we divide 74 by 2, we get a remainder of 0. Therefore, 2 is a factor of 74. If we divide 74 by 3, we get a remainder of 2. Therefore, 3 is not a factor of 74.

 

Next, we can check if 4 is a factor of 74. If we divide 74 by 4, we get a remainder of 2. Therefore, 4 is not a factor of 74. We can continue this process for all the possible factors of 74.

 

Through this process, we can find that the factors of 74 are 1, 2, 37, and 74. These are the only numbers that can divide 74 without leaving a remainder.

 

********************

10 Math Problems officially announces the release of Quick Math Solver and 10 Math Problems, Apps on Google Play Store for students around the world.

********************

********************

 

Properties of the Factors of 74

 

The factors of 74 have some interesting properties. One of the properties is that the sum of the factors of 74 is equal to 114. We can see this by adding all the factors of 74 together:

 

1 + 2 + 37 + 74 = 114

 

Another property of the factors of 74 is that the prime factors of 74 are 2 and 37 only.

 

 

Applications of the Factors of 74

 

The factors of 74 have several applications in mathematics. One of the applications is in finding the highest common factor (HCF) of two or more numbers. The HCF is the largest factor that two or more numbers have in common. For example, to find the HCF of 74 and 37, we need to find the factors of both numbers and identify the largest factor they have in common. The factors of 74 are 1, 2, 37, and 74. The factors of 37 are 1 and 37. The largest factor that they have in common is 37. Therefore, the HCF of 74 and 37 is 37.

 

Another application of the factors of 74 is in prime factorization. Prime factorization is the process of expressing a number as the product of its prime factors. The prime factors of 74 are 2 and 37, since these are the only prime numbers that can divide 74 without leaving a remainder. Therefore, we can express 74 as:

 

74 = 2 × 37

 

We can do prime factorization by division and factor tree method also. Here is the prime factorization of 74 by division method,

 

∴ 74 = 2 × 37

 

Here is the prime factorization of 74 by the factor tree method,

 

∴ 74 = 2 × 37

 

 

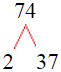
Conclusion

 

The factors of 74 are the numbers that can divide 74 without leaving a remainder. The factors of 74 are 1, 2, 37, and 74. The factors of 74 have some interesting properties, such as having a sum of 114. The factors of 74 have several applications in mathematics, such as finding the highest common factor and prime factorization.